A new idea to
obtain clean fusion energy
Home Introduction Calculations Videos Facebook Contact Sitemap
11.2 Confinement of positive ions and electrons with a static electric and magnetic field
 Various
calculations etc. of the 11e idea
Various
calculations etc. of the 11e idea
|
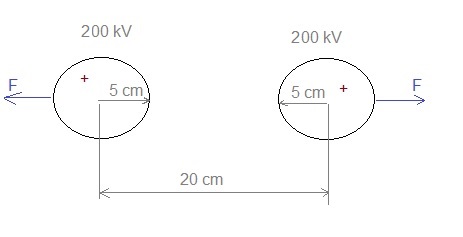
Fig. 1
Just for curiosity; calculating the force between two small spheres with diameter 5 cm, potential 200 kV and distance 20 cm: V= 9E9 . Q / r -> Q = V .r /(9E9) = 2E5/(9E9)* 0.025 = 5.56E-07 coulomb. (Q= charge of shpere; r = radius ; V = electrical potential of solitary sphere compared to infinity) F = 9E9 Q.Q / r2 = 9E9 . (5.56E-07) 2 / (0.20)2 = 0.07 N (only small)
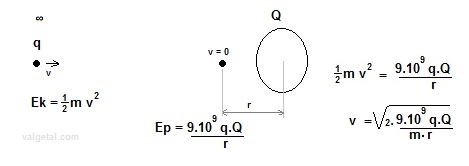
In the program we use point charges. If a D+ particle moves straight ahead (from infinity) to a point charge of 5,56E-7 Q and we want it to stop at a distance of 10 cm from this point charge, what would be the maximum speed of this particle? Fig. 2.
q= 1,6.10-19 C; m= 2 . 1,67.10-27 kg ; v =
√
(2 . 9.109
. q. Q /
( r . m ) ) This is a little big bigger than the speed needed for fusion. But very energetic particles could perhaps collide with a positive charged object in the fusion device? Perhaps it could be good that positive ions colide with the positive charged fixed object in the simulation space (vacuum chamber): they could increase its positive potential (if the objects are isolated from the voltage supply). Anyway it looks like that this requires further study....
In the next link a permanent magnet, with dimensions 11x9x2 cm and a magnetic field (Remanencia Br) of 1.3 T is sold for about 120 €, see: https://www.supermagnete.es/imanes-bloque-neodimio/bloque-magnetico-110.6mm-x-89mm-x-19.5mm-neodimio-n45-con-recubrim-epoxi_Q-111-89-20-E It would be better to use an electromagnet, which can be turned on only when we are doing an experiment.
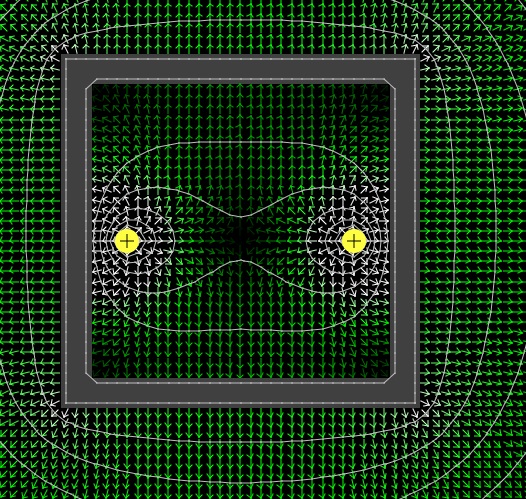
In our simulation we have positive charged point charges in an empty space. In reality they will be placed inside a sphere, as in figure 3. The positive charge will cause a regrouping of charge in the sphere (if this is conducting). This will probably decrease the electric field towards the centre of the sphere, which would be a disadvantage for our S.E.M. fusor idea... I found in http://www.falstad.com/emstatic/ an applet to simulate electric field configuration (in two dimensions). Below two screenshots: Fig. 4 Two positive charges inside a conductive box.
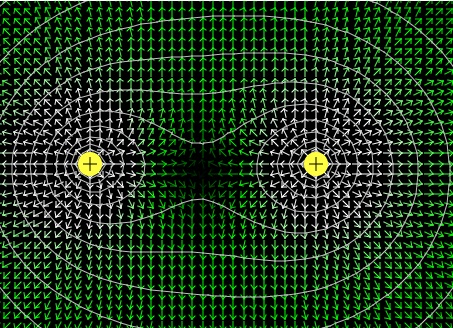
Fig. 5. Two positive charges in an empty space.
According to this applet there is not a lot of change in the electric field between the two positive charges. Fig. 6. Two positive charged conductors in a conductive box.
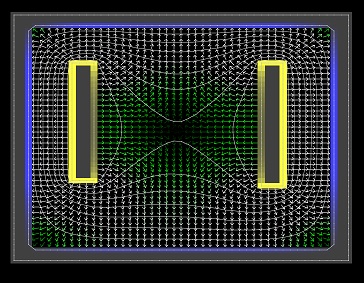
If we use positive conductors instead of point charges, according to the applet the electric field between them decreases inside the vacuum chamber.
In our program we will now simulate a conducting sphere around the
simulation space. Fig. 7. Negative point charges in a sphere around the simulation space.
We generate 648 particles (negative point charges), in two nested "for to" loops: the first one "for φ = 1 to 36" and the other one " for 1=to to 18 ( angle increment 10º ). So we get them equally distributed in a surrounding sphere for which we take a radius = 0.9 mtr. The centre of the cube is (x,y,z) = (0,5 , 0,5 , 0,5 ). The highest point of the sphere is thus (0,5 , 0,5 , 1,4) Each particle we give a charge of 5.56E-7 * 8 /648 coulomb. In the
program we can choose for the potential of the positive point charges 200 kV
(for example; this can be varied). If a point charge should be a ball with a
diameter of 5 cm, this would correspond with a charge of
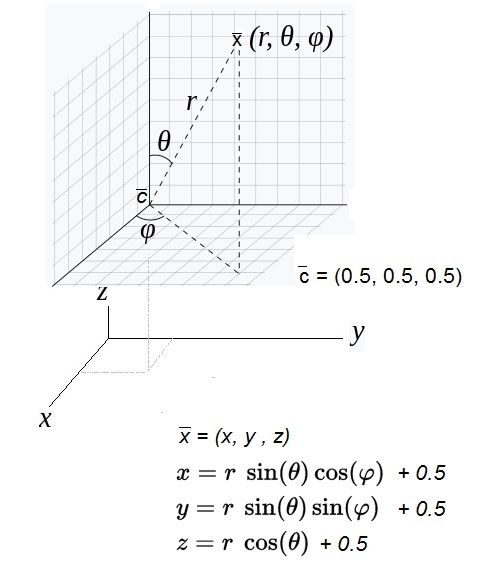
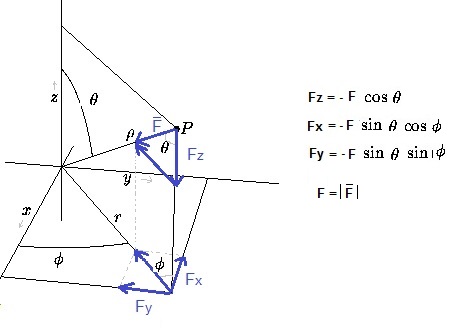
5.56E-7 Q. What is the potential of a conducting sphere, with radius 0.9 m, if its charge is 5.56E-7 . 8 C ? (inside there is no charge) V = 9E9.Q /r = 9E9 . 5.56E-7 . 8 / 0.9 = 44 kV. I will adapt the simulation program: at a radius of √ (0.52 + 0.52+ 0.52 ) = 0.87 m, there will be a kind of conducting sphere. In the program this sphere will consist of negative point charges. Before starting the simulation, after establishing the positive charge inside the simulation space, we release the negative point charges (as if it were particles). They will feel the electric field of the positive point charges and interact amongst themselves, so they start to move. They can only move on the sphere, and will move till they will feel not any longer any force. This will be similar to a real conducting sphere, in which there cannot exist any electric field. Then their position will be fixed (in reality they could be influenced by the moving ions inside the vacuum chamber/simulation space, but this would take too much computer power, and surely will be neglectable). Fig. 8. Relation between spherical and cartesian coordinates.
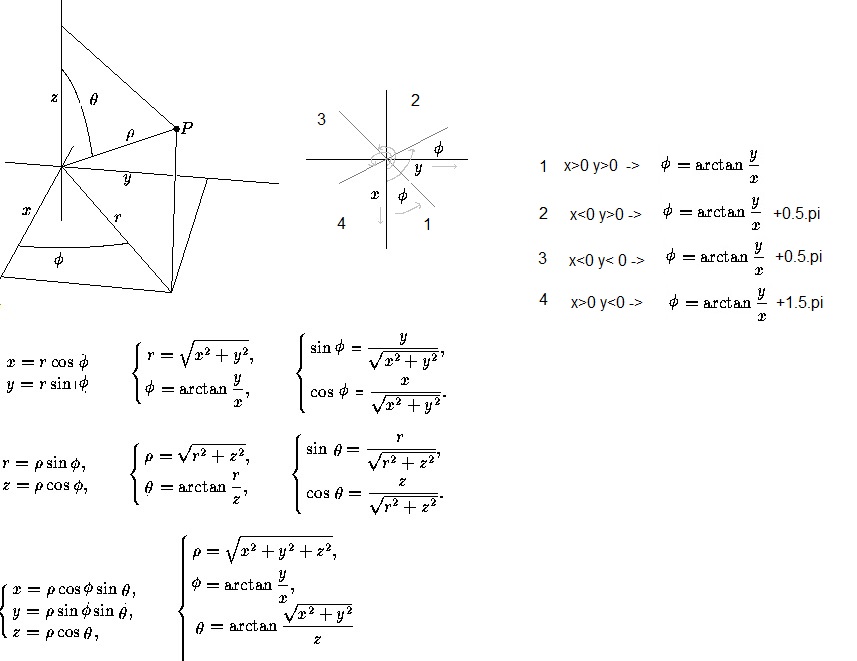
In our simulation space the centre of this space is (0.5, 0.5, 0.5); for the radius we take r = 0.9 m. (≈ √(0,52 + 0,52 + 0,52) (= 0.8660) 0º<= θ <=180º ; 0º<=φ <=360º Fig. 9. More relation between spherical and cartesian coordinates.
Fig. 10. The force on a negative charge (particle) in the conducting sphere.
In order to program the movement of the negative charge particles in the conducting sphere around the simulation space we invent a force F: when a particle leaves this sphere, then this force comes into existence and pulls this particle back to the conducting sphere. My first attempt did nto work quite well (F = factor * distance from sphere). The negative charge particles fled around. At the moment we use a simple method: Video of the distributing of the negative charge in the surrounding sphere 14/1/17: there is now a button to choose whether yes or not surrounding conducting sphere High dc voltage power supply up to 200 kV: In a "normal" fusor ( see Self made Fusor ) a pressure of about 150 millitorr (150 micron) = 150x0,1333 = 20 pascal (N/m2) is used. Torr Understanding-vacuum-measurement-units Keep thinking about this.. ☺
|
|
|