Simulation of moving electrons, hydrogen and boron ions in a magnetic field

A new idea to obtain clean fusion energy

Home Introduction Calculations Videos Facebook Contact Sitemap

10.9 Physics experiment: simulation of moving electrons, hydrogen and boron ions in a magnetic field

Computer simulation of idea 10 : calculating the kinetic and potential energy of the particles

Experiment 9

The total kinetic energy of all particles can now neither increase nor decrease (within very small limits). If it changes, then the speed of each electron is multiplied by 0.999 or by 1.001
in a repeat loop, until the total kinetic energy is again (almost) the same as the initial kinetic energy of all particles (there are only 3 H+ and 3 B+ ions, their speed is not altered,
I do not think this is important).

The looses according the Larmor Formula (about 0.1 % in 1 sec) will be neglected for the moment.

The potential energy of all particles will also be calculated.

Fig.1

The electric potential energy U of a system of two point charges q1 & q2 is equal to

(e0 = 8,854E-12 F.m^-2,r = distance between the two point charges)

Just bring q1 to infinity and calculate the work done by the Coulomb force.

The electric potential energy of a system of three point charges (see figure 1) can be calculated in a similar manner

Bring q1 to infinity and calculate the work done by the combined Coulomb force exerted by q2 & q3 on q1. Then bring q2 to infinity and calculate the work done by the Coulomb force exerted by q3 on q2.
After this all particles are at an infinite distance from each other which corresponds with U=0 .

In the program we calculate U in two repeat loops. If we had only three particles, we would calculate

So and the end we divide by 2.

Part of the program:

Ue:=0; {the total potential energy, first zero}

for i:=1 to (AmountE) do {amountE=amount of electrons}
begin
xi:=electron[i].x; {x-coordinate of electron i}
yi:=electron[i].y;
zi:=electron[i].z;
for j:=1 to AmountE do
begin
if j<>i then
begin
xj:=electron[j].x; {x-coordinate of electron j}
yj:=electron[j].y;
zj:=electron[j].z;
r:=sqrt( sqr(xi-xj)+sqr(yi-yj)+ sqr(zi-zj) ); {distance between electron i & j}

if electron[i].exists and electron[j].exists then Ue:= Ue+ K*qe*qe/r;
end; end; end;

Ue:=0.5*Ue;

Also we calculate the potential energy U between the electrons and the H+, between the electrons and the B+ ions and between the H+ and the B+ ions.
Here we do not calculate double pairs (U12 = potential energy between the first H+ and the second B+ , U21= potential energy between the second H+ and the first B+),
so here we do not divide by 2. The total potential energy of all particles is all the time stated in the program.

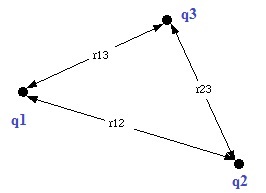
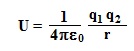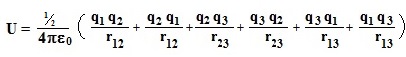Experiment 9.001 (30/6/2016) : 20 electrons, B-field= 10 gauss, initial kinetic energy of each electron (energy range) = 100 eV, beam current 0,001 nA, 3 H+ generated with initial speed=0 (in positions: (0.5, 0.5, 0.25) (0.50125, 0.50125, 0250625), (0.501246, 0.501246, 0.25125), 3 B+ generated with initial speed=0 (in positions: (0.5, 0.5, 0.75) (0.50125, 0.50125, 075188), (0.501246, 0.501246, 0.75375)

In this experiment the kinetic energy of all particles is NOT kept constant (from experiment 3 it was kept constant).

Screenshot after 1,53E-5 sec (53 min computer time)
Screenshot after 6,22E-5 sec (3h13 min computer time)

Just when the 20 e-, 3 H+ and 3 B+ were generated their total potential+kinetic energy = 3,47 E-16 J. In the first screenshot it is 6,23 E-16 J. Almost doubled! In the second screenshot 6,52 E-15 J.
Their speeds increase, probably due to the fact that the program is an aproximation of reality.

----

Experiment 9.002:
The same experiment again, but now reading the potential and the kinetic energy apart.
Initial total kinetic energy of all particles = 3,47 E-16 J , initial potential energy of all particles = 1,21 E-24 J
Screenshot after 0,00011 s Total kinetic energy = 6,2 E-14 J, total potential energy = 5,0 E-26

The kinetic energy of the particles is 178 times bigger! Because the distance between the electrons has grown, it´s understandable that the potential energy has decreased. The potential energy is, by the way, negligible compared to the kinetic energy.

---

Experiment 9.1:
50 electrons, B-field= 10 gauss, initial kinetic energy of each electron (energy range) = 100 eV, beam current 0,1 nA, 3 H+ generated with initial speed=0 (in positions: (0.5, 0.5, 0.25) (0.50125, 0.50125, 0250625), (0.501246, 0.501246, 0.25125), 3 B+ generated with initial speed=0 (in positions: (0.5, 0.5, 0.75) (0.50125, 0.50125, 075188), (0.501246, 0.501246, 0.75375).
The kinetic energy of all electrons is kept constant.

Screenshot 49 electrons generated (total potential energy of the 49 electrons = 6,9E-24 J)
Screenshot just 50 electrons generated (total potential energy of the 50 electrons = 17 E-24 J)
Video after 7,46E-5 s
When the electrons are regrouped, their mean distances become a little bit smaller, so it´s understandable that their potential energy increases. As said before, correct should be "slowly" change the B-field (during 1 s perhaps?) and simulate the movement of the electrons during this period. But 1 s real time takes about 80 year computer time (at the moment, in my own computer), so it´s not possible (at the moment..).

---

Experiment 9.22:
Screenshot 50 electrons with some vertical speed, B-field not changed (stays 10 G)
The electrons spread out in vertical direction. The electrons were given a random vertical speed (-0.01*sp) < vz < (0.01*sp) (sp = √(v_x² + v_y²) sp= speed in the horizontal plan).
The kinetic energy of all electrons is kept constant.

---

Experiment 9.23:
Screenshot 50 electrons with some vertical speed, B-field changed (from 10 G to 100 G)
Video after 3,11E-5 s
It seems to be that the electrons do NOT spread out in vertical direction. The electrons were given a random vertical speed (-0.01*sp) < vz < (0.01*sp) (sp = √(v_x² + v_y²) sp= speed in the horizontal plan)
B+ & H+ are not generated.
The kinetic energy of all particles is kept constant.
Remark: the kinetic energy is kept constant by mulitplying the components of the speed vx, vy and vz with a factor 0.999 or 1.001. It could be possible that the component vz was made zero by multiplying all the time with a factor 0.999.

---

Experiment 9.24:
Screenshot 50 electrons with some vertical speed, B-field changed (from 10 G to 100 G)
The kinetic energy Ek of all particles is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001. However, v_z is NOT mulitplied by any factor.
The electrons do now YES spread out in vertical direction. The electrons were given a random vertical speed (-0.01*sp) < v_z < (0.01*sp) (sp = √(v_x² + v_y²) sp= speed in the horizontal plan)
B+ & H+ are not generated. It´s a pity, but now they are not stopped by the magnetic field produced by themselves.

From the difference between experiment 9.22 and 9.23 we can conclude that increasing the magnetic field and let so the electrons move in small circles, seems to avoid somewhat the spreading out in the vertical direction.

It´s a pity that in experiment 9.24 they yes spreaded out in the vertical directions. We have to find out more about how much a approximation is the program (because we keep the kinetic energy of the electrons constant by multiplying the speed of the electrons with a factor..).

I checked the speed v_z of the electrons and the force Fz on the electrons in vertical directions, and they never seemed to be oposed.. So the electrons are not stopped spreading out in a vertical directions by the magnetic field produced by themselves... It´s a pity.. No, in the experiment now running I just saw that sometimes they are opposed... It´s not clear yet ??

The same experiment again, but with B field 100 - 1000 G, 100 eV, -0.0000002*sp<vz <0.0000002*sp, 0,5 m- 0.001 < z < 0,5m + 0.001 , result: electrons spreading out in vertical direction.

Remark: the speed of the electrons with 100 eV = 5,9E6 ms, 0.0000002*sp = 1,2 m/s vertical speed. I suppose this is quite a lot..

Experiment 9.25: Pobably wrong experiment, in the program B was probably not increased!
Ek is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor.
Generated 100 electrons with 100 eV. Then changed B-field from 10 G to 1000 G and the electrons distributed randomly inside the first orbiting circle. (beam current = 1 nA)

electron[i].vz:=(0.5-random)*sp*0.000000002 (2E-9) -> -5,9E-3 < vz < 5,9E-3 m/s (the initial vertical speed of the electrons)
electron[i].z:=(0.5*s/400-0.001/2+random*0.001); (s=400, side cube = 1 mtr) -> 0,4995 < z < 0,5005 (the initial vertical position varies +/- 0,5 mm )
Screenshots experiment 9.25 (after 9,76E-6 s)
Screenshots experiment 9.25 (after 15,6 E-6 s)
At the start of the experiment the total potential energy of the electrons: 3,1E-23 J < Ep < 6,8E-23 J
After 15,6E-6 s: 2,89E-23< Ep < 6,04 E -23 J
The potential energy decreases, so the electrons spread out.

After 1,86E-5 s B-field increased to 10000 G. -> 4,656 E-23< Ep < 4,653 E-23 J slowly decreasing 4,6456 E-23< Ep < 4,6409 E-23 after 1,88E-5 s

Experiment 9.252:
The same as exp. 9.25, only the B-field = 1000 G constant from the beginning.
Screenshot experiment 9.252 (after 1,9E-6 s)
The electrons "quite rapidly" spread out in vertical direction. This could be explained because the electrons are from the beginning already more close together than in exp. 9.25, so the Coulomb repelling forces will be bigger.

Experiment 9.253:
The same as exp. 9.25, only the B-field = 10 G constant from the beginning.
Screenshot experiment 9.253 (after 6,64E-6 s)
Screenshot experiment 9.253 (after 7,63E-6 s)

The electrons spread out in vertical direction.

Experiment 9.254: Probably wrong experiment, in the program B was probably increased!
The same as exp. 9.25, but now the B-field = 10 G -> 10000 G (wrong experiment, in the program B was not realy increased!)
Screenshot experiment 9.254 (after 2,33E-6 s)
Screenshot experiment 9.254 (after 1,64E-5 s)
Video exp 9.254
t=1,58E-7 -> 2,08E-23 < Ep < 8,05 E-23
t=1,64E-5 -> 2,051E-23 < Ep < 7,26E-23

Experiment 9.3:

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor.
Generated 100 electrons with 100 eV. Then changed B-field from 10 G to 1000 G and the electrons distributed randomly inside the first orbiting circle. (beam current = 0,1 nA)

At the start of the experiment the total potential energy of the electrons: 8,67 E-23 J < Ep < 8,859 E-23 J
Screenshot experiment 9.3 just before regrouping electrons 8,7 E-23 < Ep < 8,86 E-23
Screenshot experiment 9.3 after 1,38E-6 s
Screenshot experiment 9.3 after 1,59E-5 s 5,4 < Ep < 5,5 E-23

The potential energy of the electrons decreases. It is clearly to see in the last screenshot that the electrons have spread out. The vertical speeds of the electrons have also increased (see screenshot, from a couple of m/s till a couple of 100 m/s to even more than 1000 m/s.

---

Experiment 9.31:

The same as experiment 9.3, but now the magnetic field changes from B=100 G to B= 1 T.
Screenshot experiment 9.31 after 3,78E-6 s

At the start of the experiment Ep= 2,76 E-21 J, after 3,78E-6 s Ep= 4,8E-22 J. The potential energy of the electrons has decreased. The electrons have spread out.

----

Experiment 9.33:

electron[i].vz:=(0.5-random)*sp*0.0000000002; (2E-10)
electron[i].z:=(0.5*s/400-0.0001/2+random*0.0001); (the initial vertical position varies +/- 0,05 mm )
200 electrons, B-field 10 G to 1000 G, electrons distributed randomly inside the first orbiting circle.
Screenshot experiment 9.33 after 2,76E-6 s
Screenshot experiment 9.33 after 5,14E-6 s

At the start of the experiment Ep= about 2,87 E-22 J, after 2,76 E-6 s Ep= about 2.68 E-22 J. The potential energy of the electrons has decreased. The electrons have spread out.

---

Experiment 9.34:

electron[i].vz:=(0.5-random)*sp*0.0000000002; (2E-10)
electron[i].z:=(0.5*s/400-0.0001/2+random*0.0001); (the initial vertical position varies +/- 0,05 mm )
200 electrons, B-field 10 G constant
Screenshot experiment 9.34 after 2,81 E-6 s
Screenshot experiment 9.34 after 5,24 E-6 s

At the start of the experiment Ep= about 2,5448 E-22 J, after 2,81 E-6 s Ep= about 2.543 E-22 J. The potential energy of the electrons has decreased. The electrons have spread out.

---

Conclusion so far:

We want that the electrons stay in the centre of the vacuum chamber (the cube in the simulation program). We try this by applying the simple trick "increasing the magnetic field so that the electrons start to move in small circles and are glued together by the magnetic fields they generate themeselves". Intuitive explanation of this in experiment6 . In experiment 9.3, 9.31 & 9.33 the electrons have spread out. The "trick" did not work... It's a pity..

---

Experiment 9.35:

electron[i].vz:=(0.5-random)*sp*0.00000000002; 2E-11 m/s -> -5,9E-5 < vz < 5,9E-5 m/s (the initial vertical speed of the electrons)
electron[i].z:=(0.5*s/400-0.00001/2+random*0.00001); (the initial vertical position varies +/- 0,005 mm )

Screenshot exp. 9.35 after 1,01 E-5 s

At the start of the experiment Ep= about 7,2 E-23 J, after 1,01 E-5 s Ep= about 6,3 E-23 J. The potential energy of the electrons has decreased. The electrons have spread out.

---

Experiment 9.36:

At the start of the experiment Ep= about 6,6 E-23 J, after 1,1 E-5 s Ep= about 4,07 E-23 J. The potential energy of the electrons has decreased. The electrons have spread out.

Screenshot exp. 9.36 100 e- 10 G

---

In exp. 9.36 the electrons have spread out a little bit more than in experiment 9.35. Probably because they are closer together.

---

Experiment 9.37:

Screenshots experiment 9.37 after 3 E-5
Video experiment 9.37 after 3 E-5 s

At the start of the experiment Ep= about 8,4 E-23 J, after 3 E-5 s Ep= about 4,2 E-23 J. The potential energy of the electrons has decreased. The electrons have spread out.
Curious that one electrons up and one down have started to move in larger circles (probable higher speeds).

---

Experiment 9.38:

Screenshot experiment 9.38 after 3 E-5

At the start of the experiment Ep= about 6,2 E-23 J, after 3 E-5 s Ep= about 2,7 E-23 J. The potential energy of the electrons has decreased. The electrons have spread out.

Experiment 9.39: (error in program, vx:=vx+((Fx+Fxi)/(2*m))*dt; Fxi=0, should be vx:=vx+((Fx)/(m))*dt; (that is probably why not in the middle..)

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor. (0,1 nA)
Generated 100 electrons with 100 eV. Then slowly changed B-field from 10 G to 1000 G in small steps.

if (amountE=100) and not (Already) then begin
if B<1000E-4 then B:=B+0.0000001 else Already:=true;

electron[i].vz:=(0.5-random)*sp*0.0000000002; 2E-10 m/s -> -5,9E-4 < vz < 5,9E-4 m/s (the initial vertical speed of the electrons)
electron[i].z:=(0.5*s/400-0.0001/2+random*0.0001); (the initial vertical position varies +/- 0,05 mm )

Screenshot experiment 9.39 after 1,86 E-6 (B-field just became 1000 G)
Screenshot experiment 9.39 after 6,19 E-6

Experiment 9.392: (error in program, vx:=vx+((Fx+Fxi)/(2*m))*dt; Fxi=0, should be vx:=vx+((Fx)/(m))*dt; (that is probably why not in the middle..)

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor. (0,1 nA)
Generated 200 electrons with 1000 eV. Then slowly changed B-field from 10 G to 1000 G in small steps.

if (amountE=200) and not (Already) then begin
if B<1000E-4 then B:=B+0.0000001 else Already:=true;

Screenshot experiment 9.392 after 4,58 E-6 s

Experiment 9.393:

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor. (0,1 nA)
Generated 100 electrons with 100 eV. Then slowly changed B-field from 10 G to 1000 G in small steps.

if (amountE=100) and not (Already) then begin
if B<1000E-4 then B:=B+0.0000001 else Already:=true;

{Bh:=B + 2r1 + 10r2 (r1= radius in xy-plane, r2=vertical distance from center cube, at side r1=0,5 & r2=0,5 m)

electron[i].vz:=(0.5-random)*sp*0.00000000002; 2E-11 m/s -> -5,9E-5 < vz < 5,9E-5 m/s (the initial vertical speed of the electrons)
electron[i].z:=(0.5*s/400-0.0001/2+random*0.00001); (the initial vertical position varies +/- 0,05 mm )

Screenshot experiment 9.393 after 1,7 E-6 (B-field 880 G, not yet 1000 G)
The electrons did spread out already quite a lot.

---

Experiment 9.394:

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor. (0,1 nA)
Generated 200 electrons with 100 eV. Then slowly changed B-field from 10 G to 1000 G in small steps.

if (amountE=200) and not (Already) then begin
if B<1000E-4 then B:=B+0.0000001 else Already:=true;

{Bh:=B + 2r1 + 10r2 (r1= radius in xy-plane, r2=vertical distance from center cube, at side r1=0,5 & r2=0,5 m)
B at the sides stronger. B up and down also stronger.
But after generated 200 e- B-field constant?

Screenshot experiment 9.394 after 3,03 E-6
Screenshots experiment 9.394 after 6.05 E-6

The electrons did spread out quite a lot.

---

Experiment 9.395:

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor. (0,01 nA)
Generated 50 electrons with 100 eV. Then slowly changed B-field from 10 G to 1000 G in small steps.

if (amountE=50) and not (Already) then begin
if B<1000E-4 then B:=B+0.0000001 else Already:=true;

{Bh:=B(1 + 2r1 + 10r2) (r1= radius in xy-plane, r2=vertical distance from center cube, at side r1=0,5 & r2=0,5 m)
B at the sides stronger. B up and down also stronger.

Screenshot experiment 9.395 1.7 E-5 s

The electrons did spread out quite a lot.

---

Experiment 9.396:

The total kinetic energy Ek of the electrons is kept constant by mulitplying the components of the speed v_x and v_y with a factor 0.999 or 1.001; v_z is NOT mulitplied by any factor. (0,1 nA)
Generated 100 electrons with 1000 eV. Then slowly changed B-field from 10 G to 1000 G in small steps.

if (amountE=100) and not (Already) then begin
if B<1000E-4 then B:=B+0.0000001 else Already:=true;

{Bh:=B(1 + 2r1 + 10r2) (r1= radius in xy-plane, r2=vertical distance from center cube, at side r1=0,5 & r2=0,5 m)
B at the sides stronger. B up and down also stronger.

Screenshots experiment 9.396 7.99 E-6 s
Screenshot experiment 9.396 1,2 E-5 s It seems to be that the electrons do not spread out.....
(one electron moving very fast, the others seem not to move, anyway as can be seen in the screen)

The same experiment again, starting from t=0:

Screenshot experiment 9.396 2.02E-5 s

The electrons do spread out...
The B-field was reduced to 0,1 G. Only one electron started to move in a wide orbit. The other ones seemed not to move, what means they had a very small speed. Probably because the procedure that kept the total kinetic energy constant by reducing (or augmenting) the speed of all electrons, did reduce their speed (in the x-y plane) to zero (except for one electron).

---

Experiment 10:

To make the simulation more accurate we implemented the Leapfrog method,

see experiment 10

Back to main page

Facebook
Sem-fusor.com

Rinze Joustra www.valgetal.com