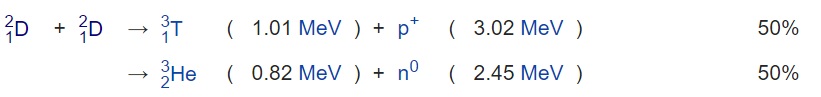A new idea to obtain clean fusion energy
Home Introduction Calculations Videos Facebook Contact Sitemap
11. Confinement of positive ions and electrons with a static electric and magnetic field
|
Main page Calculations (Explained in chronological order, how I myself discovered everything step by step....)
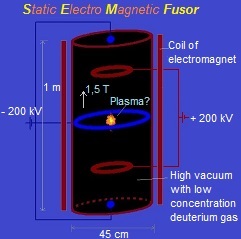
The goal is to design a kind of fusor ( Wikipedia.org/wiki/Fusor ). But instead of a fixed inner grid, which causes losses, we try to confine positive H+ and B+ ions with a static electric field and a static magnetic field.
We'll use our computer simulation program,
as described in:
10b computer simulation Let us
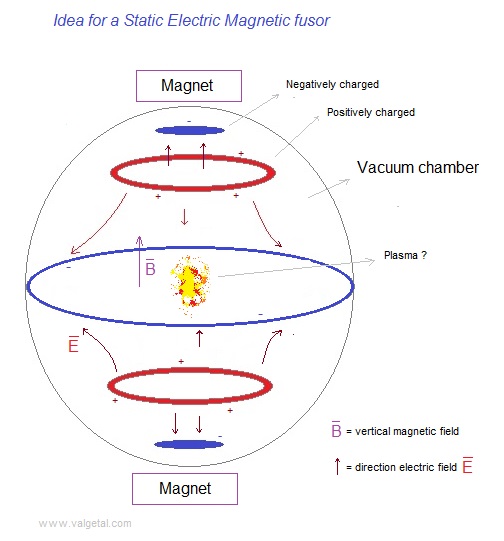
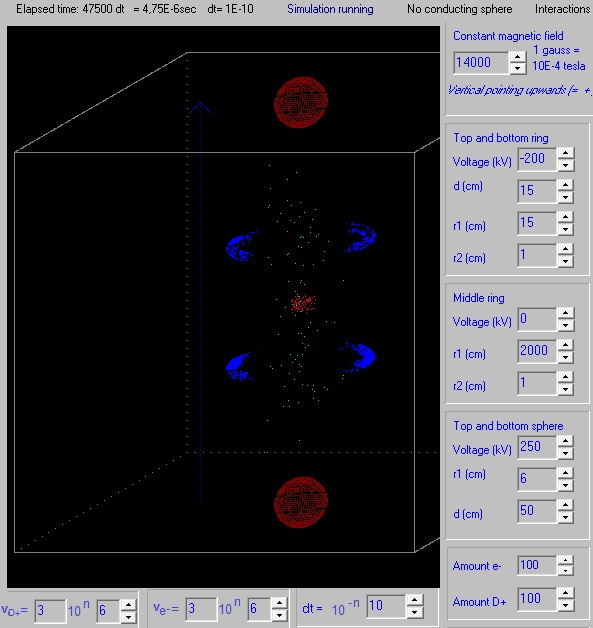
simulate the following device: Fig.
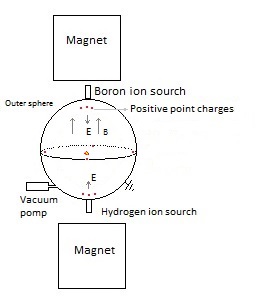
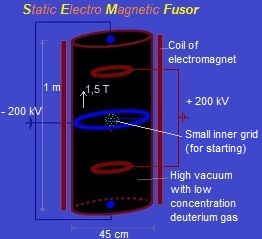
1. Schematic representation of a Static Electro Magnetic fusion device (
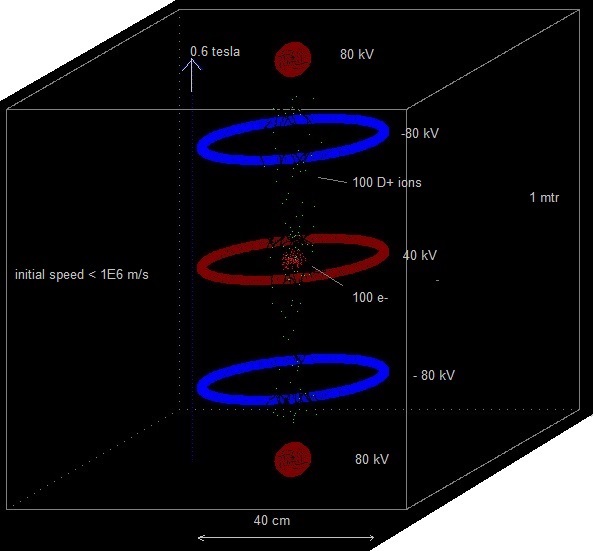
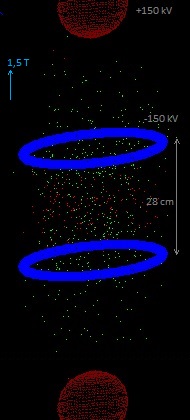
The sphere (vacuum chamber) has been pumped vacuum and is earthed. Above and under the sphere (or around) a magnet is placed which generates a vertical magnetic field inside the sphere. We'll try out several magnetic field configurations in the computer program. An electric field is created by placing eight point charges: four near the top and four near the bottom. In a real apparatus this could be done different (perhaps with rings? see applet), but in order to simulate it easily in our computer program we'll do it at the moment in this way (with point charges). In the middle of each side is also a point charge placed. Fig. 2. The simulation space, with four positive point charges above and four under ( and one in each side; not in the drawing).
Several experiments are performed with the simulation program, see: 11.1 Experiments 11.1 till 11.6 and Video Youtube The ions have a random initial speed up to 0,5E6 m/s in all directions.
Potential of an electrical charged sphere:
V= 9E9. Q /r
(r=radius of sphere, Q=charge of sphere, V=electrical potential of sphere) The movement of the positive ions is simulated using Leap-frog integration (see 10.1 experiment10 ). The ions interact amongst themselves and with the electric and magnetic field applying the Coulomb and Biot-Savart formulism ( non-relativistic).
To check the correctness of the simulation, we will calculate the total energy of all particles.
The kinetic energy of all moving particles is calculated (electrons, H+ and
B+ ions). Part of the program:
See: 11.1 Experiment_11.6 and 11.7 The positive charge of each fixed point charge is: 5.56E-7 Q (100 kV for a sphere with diameter 10 cm), the magnetic field constant 1 tesla, generated 200 H+ and 200 B+ with initial random speed < 0,5E6 m/s. With dt=1E-9 s no ions escaped and the total energy of the particles stayed constant.
When positive charged ions collide, some of them can get higher speeds and could escape. This could perhaps be prevented by two charged grids, as shown in figure 3: Fig. 3. Schematic representation of an electrostatic magnetic fusion device with two grids near the outer wall
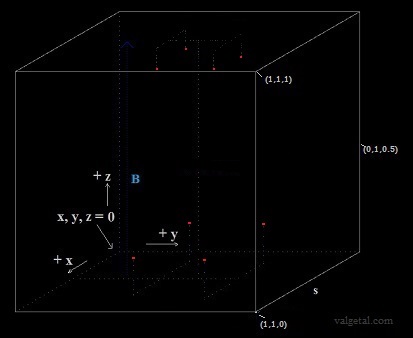
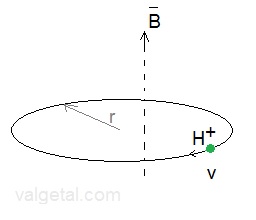
The negatively charged grid must be close enough, so it does not produce a "negative" electric field inside the sphere. But also it must be open enough (with holes), to prevent that too much positive ions collide with it, producing unwanted losses. Our simulation space is a cube with a side of 1 m. Fig. 4. Moving H+ ion in a magnetic field B.
With which speed do deuterium ions fuse? (see
also:
Droom11.16.htm
) We look a little further:
In
euro-fusion.org
a temperature of about 450E6 degrees C is /was) mentioned for D-D
fusion reaction to occur.
(Boltzmann constant = 1.38064852 × 10-23 m2 kg
s-2 K-1)
Also in hyperphysics it is suggested that the currently attainable particle energies in thermonuclear reactors is in the range 1-10keV, corresponding to 0.77E7 K- 0.77E8 K. Filling in 0.77E8 K in hyperphysics we get v ≈ 1E6 m/s (for a deuterium ion).These temperature-speed calculations are not very correct/detailed, but anyway we get some idea about it. It seems to be that with a magnetic field of 1 tesla we could more or less confine D+ particles up to about 2,4E7 m/s. This is ten times higher than the speed needed to fuse ... So the confinement to the sides seems to be okay.In the simulation program we gave the ions an initial random speed in all directions of 0.5 E6 m/s . This is 25 % of the speed needed for D+ to fuse. If we increase this initial speed, some particles escape upwards and downwards (with B=1 T and 200 kV).
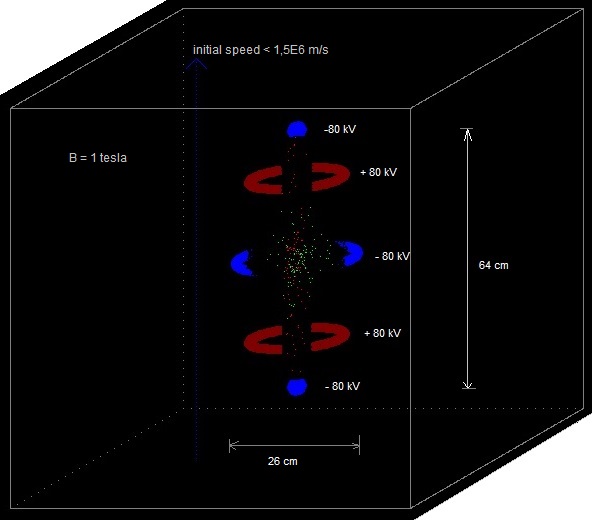
We increased the electric field by creating more positive point charges above and increasing the voltage to 300 kV; applied a magnetic field of 1,5 tesla; generated 20 H+ and 20 B+ ions with an initial speed up to 1,5E6 m/s in all directions, and the ions stayed ... confined! See 11.1 Exp. 11.7 Instead of hydrogen and boron, we will use now only deuterium ions. Massa D+ = 2 x massa H+ . B=1 tesla and 200 kV, initial speed up to 1,5E6 m/s. The ions stayed confined. Also with B=0,7 tesla and 90 kV they stayed confined.
Discussion about confinement of positive ions in fusor.net
For fusion to occur, it seems to be necessary to have an amount of
10^18 ions per
cubic meter= 1E18 . 1,6E-19 C = 1,6 C ( a lot of charge).
How many ions of D+ we need to fuse to get, for example, 100 kWh?
( see: Wikipedia ) Per ion about 3,7/2 MeV is liberated = 1,8E6 . 1,6E-19 J = 2,9E-13
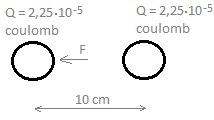
J 100 kWh -> 12,3E20 ions -> 4,1E-6 kg = 4,1 E-3 gram of deuterium (1 gram deuterium = 8,78E10 J =2283 ltr diesel). --- To get an idea about the charge: 100 W = 100 J/s -> 3,4E14 ions/s 3,4E14 ions = 3,4E14 . 1,6E-19 = 5,5 E-5 coulomb -> (5,5E-5)/ (5.56E-7) => charge of 198 small spheres with diameter 5 cm & 200 kV Let's imagine two spheres, each sphere with half this charge, at a distance of 10 cm:
They will exert a force on each other: F = 9.109 . 2,25.10-5 . 2,25.10-5 / 0,12 = 455,6 N ≈ 46 kgf 200kV x 5,5 E-5 C/s = 11 W ---
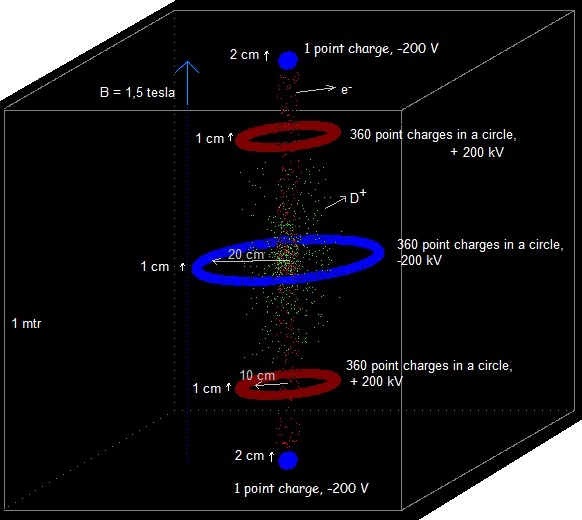
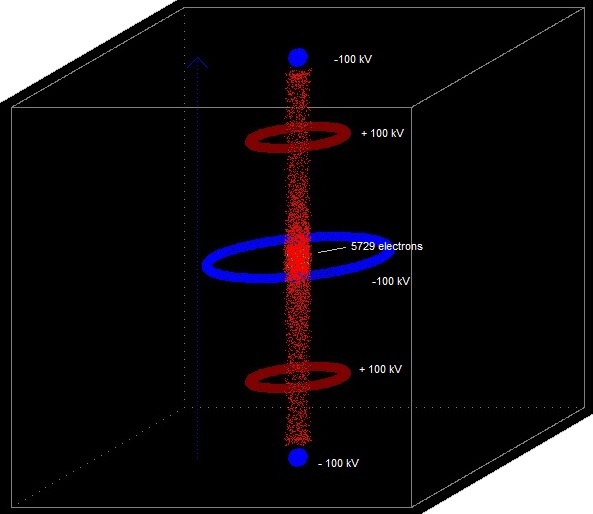
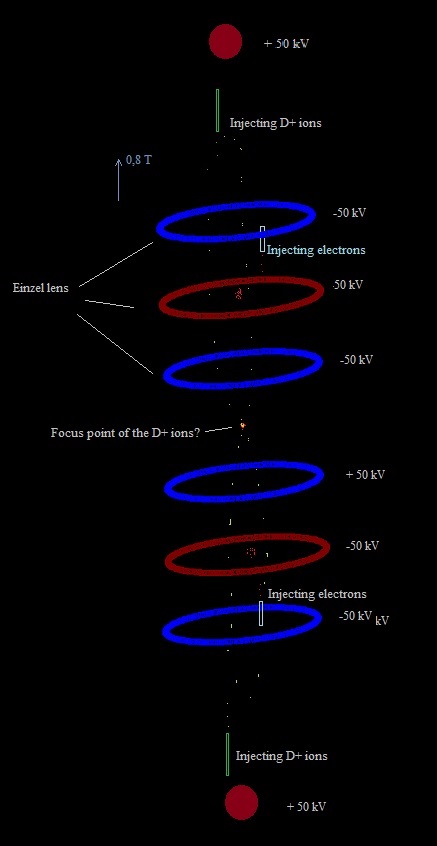
We will put some negative point charges in the centre of the top and the bottom side.
I moved the negative point charges in the top side 20 cm upwards, and the ones in the bottom side 20 cm downwards. See Exp. 11.10 b,c and Video Youtube exp. 11.10c D+ ions and electrons got an initial random speed < 1,5E6 m/s (about 2E6 is needed for fusion) .
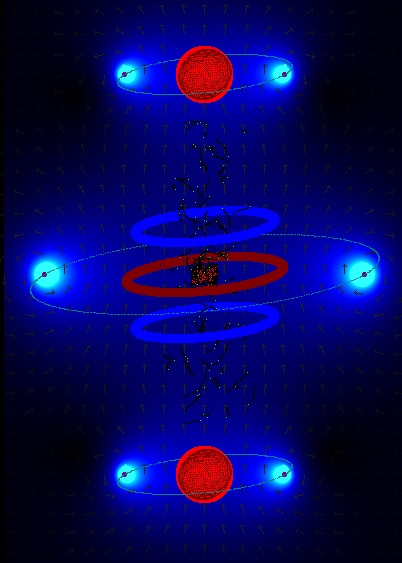
How we could give this simulation shape in the real world? Fig. 5. Possible device that corresponds with the simulation (S.E.M. fusor).
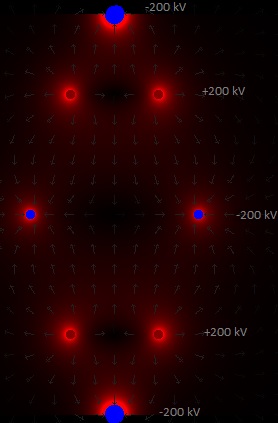
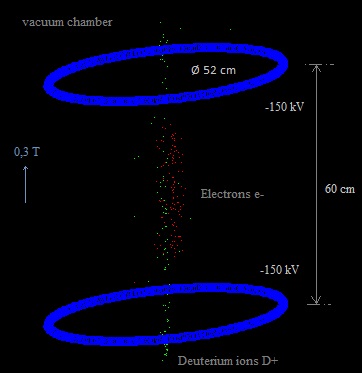
Cross section of the electric field according www.falstad.com. Possible modus operandi: The vacuum chamber is pumped empty. Only some deuterium gas is discharged inside. (The best way to do this should be investigated: perhaps most favourable is to inject it along the vertical centre line.) This gas is ionized (I suppose) into D+ ions and electrons because of the electric field . The electrons (more or less near the vertical centre line) are attracted by the two positively charged rings and move upwards and downwards in a spiral-shaped path. The vertical magnetic field of 1 tesla prevents them to escape sideward. Once they move through the ring they will be repelled by the negatively charged ellipsoid and move back towards the centre. In this way the electrons will oscillate between the blue ellipsoids and the centre of the vacuum chamber. (this is what happens in the simulation) The D+ ions (more or less near the vertical centre line) are repelled by the two positively charged rings and will vertically oscillate around the centre of the vacuum chamber, also in a spiral-shaped path. (this is what happens in the simulation) In a "traditional" fusor the positive ions move towards the centre (a point). However, only when they are outside the inner grid they feel the force towards the centre. Once they are inside the inner grid (and they have not collided with it), they will not feel this force any longer (if I am not wrong). In our S.E.M. fusor the D+ will oscillate in a vertical movement (al least in the simulation..). Will the same happen as in a traditional fusor: the positive D+ ions are confined and attracted towards the centre; they collide between each other; some of them get as a result of these collisions higher speeds; some ions with higher speeds collide between each other and fuse..... ? In the simulation there are only a few particles (it is not possible to have more than a couple of hundreds, otherwise it's takes too much memory of the computer and the simulation speed becomes too small). In the program it is possible to turn on and off the interaction between the particles. When there are only a few particles, it hardly influences the speed of the simulation, but when there are more particles, more then 100, then the simulation is running faster with the interaction turned of. In the real world possibly a cloud of electrons and deuterium ions (mixed together: a plasma), will be confined more or less in the centre of the vacuum chamber. Maybe we should construct this new type of fusor, and see what happens.. At the moment I will continue with the simulation program: visualize the electric field, simulate charged ring and ellipsoid conductors , do more experiments.. 14/1/17: there is now a button to choose whether yes or not to have a surrounding conducting sphere
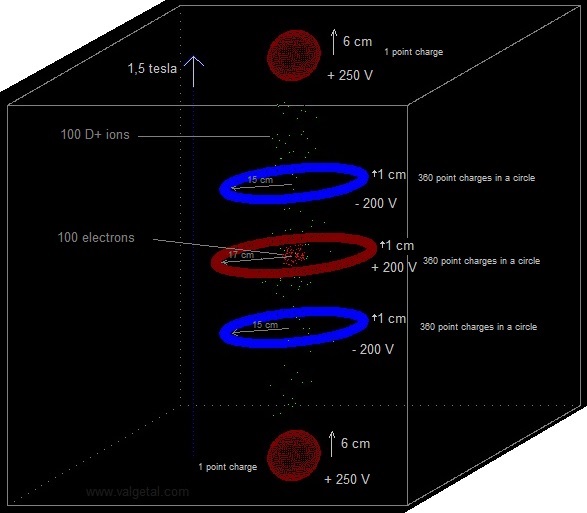
11.1 Experiment 11.11 If the point charges in
the sides are positive, the D+ ions escape upwards and downwards. Two positive rings, one negative ring and two negative charged spheres
have been programmed, see: Fig. 6. The simulation space in experiment 11.14a. With an initial random speed < 3E6 m/s (!) the D+ and the e- kept confined in the simulation space (during the short simulation time). Although the simulation had been running about 48 hrs, the real
simulation time is very small: 1,2E-5 s. The voltages can also be reversed: The electrons are now more confined in the centre, but the D+ ions spread more out in the vertical direction, although they do not escape (during the short simulation time). The D+ ions seem to obtain more speed in this configuration (= higher temperature). This would be an advantage to obtain fusion.. Furthermore, the electrons perhaps form a kind of virtual cathode that will attract the D+ ions towards the centre. Fig. 7b.
In the experiment of figure 7b. the positive middle ring has been deleted. The electrons still stay confined and the D+ ions will obtain an higher speed in the centre (I suppose) compared with the configuration of figure 7a. Higher speed (is higher temperature) means more change of nuclear fusion.. However the confinement of the electrons is less compared with the configuration with a middle ring.
Fig. 8. Another drawing of a possible design of the SEM fusor Searching for similar already existing devices:
The Penning fusion experiment
2e link
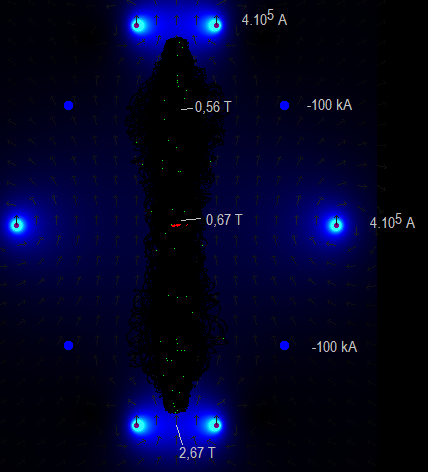
3e link 11.4 About creating the magnetic field Fig. 9. Generating more than 5000 electrons (exp. 11.18) The simulation program got stuck (did not proceed any longer) with this
amount of particles. Fig. 10. Giving the particles less initial speed allows less voltages and smaller dimensions (exp. 11.19) Fig. 11. Reversed polarities and less initial speed, allowing less voltages and smaller dimensions (exp. 11.20)
Maybe we could use a small inner grid ( as in a Farnsworth fusor) to start the operation . Fig. 12. SEM fusor with small inner starting grid
What polarity is the best to be used we should investigate. (fig. 6 or fig. 7). We could construct an experimental SEM fusor with the possibility to reverse the polarities and try out. Possible modus operandi: Plenty of experimental work could be done to try, find out.... The big question: will fusion take place, as in the Farnsworth fusor? Fig. 12. The electric field. The electric field can now be visualized, --- The electrons represent the greatest loss and maximal heating component
of the traditional fusor. They are accelerated just like the deuterium ions, but
towards the shell wall. They slam into it producing x-rays and accounting
for the bulk of the heating of the outer shell wall. See: In our SEM fusor the electrons stay also confined! --- Is it possible to charge the rings and spheres with 200 kV? Let's take a sphere with a radius of 1 cm: In www.researchgate.net/ is mentioned "generally, for distances of about 1 cm and pressures of about 10^-7 torr the dielectric strength is ranging from 200 kV/cm to 400 kV/cm. Even larger values are possible for lower pressures". In Wikipedia.org "Field emission in pure metals occurs in high electric fields: the gradients are typically higher than 1 gigavolt per metre". So it seems to be that we will not have problems with dielectric breakdown or field emission, if our fusor has a good vacuum. --- Applying a mirror magnetic field to the SEM fusor and see if this will improve it. See 11.9 Magnetic mirror simulation. Fig. 13. Applying a magnetic mirror field. By doing so we can decrease (a little bit) the voltages of the charged rings and spheres. --- It is not possible to simulate more than a couple of hundred particles,
because lack of computer power. This example demonstrates that we can not simply represent a group of particles by a few particles: Droom11.18.htm ---- In alpha.web.cern.ch/penningtrap a device a little bit simular to the SEM fusor is used, but not for fusion. Here the goal is to trap antiprotons and positrons in order to produce antihydrogen. According to them the electrons cool down due to cyclotron_radiation . "Antiprotons, however, are far more massive. It would take antiprotons over 300 years of sitting in a 1 Tesla magnetic field to cool through cyclotron radiation alone!" That the electrons cool down in the SEM fusor is only favorable, I think. So they form even better a negative cloud: a virtual cathode (I suppose). The protons however should be hot, move with high speeds in order to be able to fuse. -- In https://en.wikipedia.org/wiki/Solar_core "At the center of the Sun, fusion power is estimated by models to be about 276.5 watts/m3. Despite its intense temperature, the peak power generating density of the core overall is similar to an active compost heap, and is lower than the power density produced by the metabolism of an adult human." And here: coldfusionnow.org/power-equivalent-to-the-sun-we-already-have-it/ This is not very promising... --- Will fusion take place? (various calculations) --- Fig. 14. Generating the D+ ions and the
electrons all over the vacuum chamber, Some D+ ions obtain speeds till 2,3E6 m/s (more or less in the centre region). --- An example that demonstrates that we cannot simply representate a group of particles by a few one: Droom11.18.htm --- Duinlab\Duin1.html -> quite a different approach --- If we inject and confine boron ions B+ , hydrogen ions H+ and electrons, perhaps we achieve the reaction: 115B + 11H -> 3 42He + 8,68 MeV An advantage of this fusion reaction with boron is that it (almost) not produces neutrons, which are dangerous and noxious. See: Experiment_11.17.9 --- The simpler the design the
better, I suppose.. The next simulation was with only two negatively charged rings: Fig. 15. --- Accelerating D+ ions with a voltage difference of 900 V gives them a speed of 3. 105 m/s . See Speed-voltage-temperature calculations --- --- An idea is perhaps a configuration with 6 rings: Fig. 16. --- An design that has perhaps some similarities with the
SEM fusor: --- A new idea (applying a kind of reversed magnetic bottle) --- Will voltage breakdown occur in the Sem Fusor? ---- Injecting the electrons from the side, horizontally The interaction of the magnetic and the electric field results in a bit strange movement of the electrons: Fig. 17. With only a magnetic field they move in small circels around the vertical field lines. But if also an electric field is applied, produced by two negatively charged rings, they move also in a "big circle". And the radius of this big circle seems to be, more or less, independent of the strength of the magnetic field and the voltage of the rings. Quite curious.. Recording of various experiments in youtube ----------------- Some more experiments with the configuration with only two negatively charged rings: Fig. 18. When a kind of "Bremsstrahlung" is introduced in the program (reducing
the speed of the electrons), ---------------------- A first experiment to do could be: See also: Droom17.htm Better would be to inject also the D+ ions into the vacuum chamber. See also Droom15.htm#Conclusion, so far: Or perhaps we inject a neutral beam from the top and from the bottom which collides in the centre, where D+ and electrons are formed: Droom16.htm (simulation generating the D+ and electrons in the centre) ----------------------------------------- Exp. 11.9.7. Two negatively charged rings, D+ and e- injected from below to
up. -----------------------< Conclusion so far: Doubts: How many electrons will be confined in the centre? Will they form a virtual negative electrode, which could atract the positive deuterium ions? Will they neutralize with D+ ions? Will the deuterium ions sufficiently be confined by the magnetic field, the charged rings and the electron cloud in the centre? And will some of them obtain such high speeds so that fusion can take place? A bit similar as in a Farnsworth Fusor ? And if fusion occurs, will there be a net energy gain? The simulation program only demonstrates that we can confine a couple of hundred of deuterium ions and electrons in a static electric and magnetic field. But it would be very interesting to perform real systematic experiments. Keep thinking about this.. ☺
With about 2 millions (dollar or euro) we could buy a building for a lab, magnet, instruments... and do real experiments. The fusion experiment ITER in the south of France costs about 20000 millions... so 2 millions isn´t so much J At the moment I have started with doing "small experiments", see: Trying to do real systematic (small) experiments (ask me password)
Experiments with an electroscope Creating a ray of electrons in a vacuum glass bottle
|
|||||||||||||
|
|