Experiments with simulation of confinement of ions in a static electromagnetic field

11.15 Confinement of positive ions and electrons with a static electric and magnetic field

Increasing both the mass and the charge of the particles to make it possible to "simulate" millions of ions and electrons

Because lack of computer power it is not possible to simulate more than a couple of hundreds of particles.

But what we can do is increase both the mass and the charge of the ions and electrons: we will create "particles" consisting of millions and millions of electrons and deuterium ions.
Each "particle" corresponds then to a "group of particles". This new model is quite an approximation of reality, but it will be curious to see what happens in the simulation.

The more electrons are located inside the vacuum chamber (between the rings), the more they will repel each other:
But the positive deuterium ions that are also located inside the vacuum chamber will (probably) neutralize the negative charge of the electrons (in some degree..).

Experiment 11.15a

Fig.1.

A kind of magnetic mirror field is generated by the three current rings and an electric field by the charged rings and spheres.

The program generated 200 "red dots"; each red dot is a "particle" with a charge of 1E10 * -1,6E-19 C (charge of an electron), and with a mass of 1E10 * 9,1E-31 kg (mass of an electron).
Also it generated 200 "green dots"; each green dot is a "particle" with a charge of 1E10 * +1,6E-19 C (charge of a D+ ion), and with a mass of 1E10 * 2 * 1,67E-27 kg (mass of a D+ ion).
The speed of the "particles" is random up to 3E6 m/s.

The charge of one red dot = 1E10 * -1,6E-19 C = -1,6E-9 C.

During the short simulation time some electrons and deuterium ions escaped, but a great part of them stay confined. (I should have to add a procedure in the program that counts the amount of escaped particles..).

To get an idea about the quantity of electrons generated:

In the following link an electron gun is sold with an energy range: 1 eV to 100 keV and a beam current range: 1 nA to 20 mA kimballphysics.com/electron-gun-systems

1.10^-9A = 1.10^-9C/s ~ 1.10^-9C/s / (1,6.10^-19C) = 6,3. 10⁹electrons/s

If the electrons would be generated with an electron gun that produces about 6,3. 10⁹electrons/ sec, we needed 200*1E10/(6,3. 10^{9) =} 317 s = 5,3 min

According the simulation program the charge of the blue ring at - 200 kV is - 2,38E-6 C.

So the total negative charge of the 200 red dots (the electron cloud) is 13 % of the charge of one ring.

Fig.2.

The same experiment after a little bit more time.

Experiment 11.15b

Fig.3.

A constant magnetic field of 1,5 tesla. A part of the electrons and D+ ions escaped. From t=5,65E-5 s to t=5,72E-5 s the maximum radius of the electrons stay the same. This is good. The maximum radius of the D+ increased however. Problable due to some escaped D+.

Experiment 11.15c

Fig.4.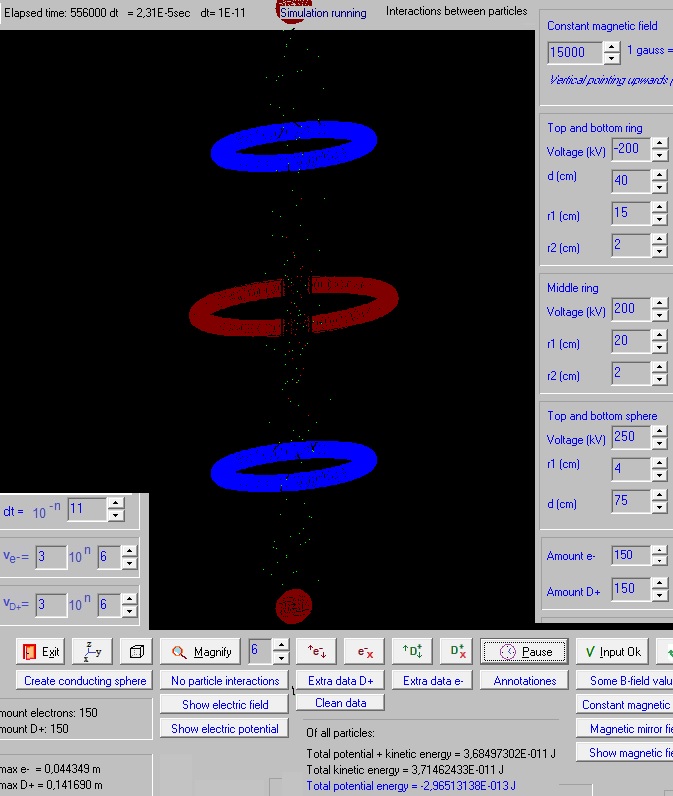

A constant magnetic field of 1,5 tesla. After 2,31E-5 s still about 43 electrons and 100 D+ ions confined (generated 150 of each type).

The distribution of the D+ ions is quite uniform (between the two positive charged spheres), and the distribution of the e- is also quite uniform between the two negative charged rings.

Many particles escape. The interaction between the particles can be shut off: the particles stay then nice confined.

Experiment 11.15d

Fig.5.

Generated 50 x 1E10 electrons and 50x1E10 D+ ions.

During the time lapse of 1,07E-6 s 3 D+ and a couple of e- escaped.

Experiment 11.15e

Fig.6.

Generated 200 x 1E9 electrons and 200x1E9 D+ ions.

During the time lapse of 4,9E-7 s only a few particles escaped.

200 x 1E9 electrons = 3,2E-8 C -> an electro gun of 1 nA would need 32 s to generate them.

200x1E9 D+ ions * 2 * 1,67E-27 kg = 6,68 E-16 kg (about nihil).

0,01 gram of D+ ions -> 0,01E-3 / (2 * 1,67E-27) = 3,0 E21 ions = 300 E19 ions.

Experiment 11.15e

Fig.7.

Generated 200 x 1E11 electrons and 200 x 1E11 D+ ions with initial speed = 0.

As shown in fig. 7 the electrons obtain very high speeds, probably due to interactions between the other particles.
Obviously the simulation is now not good.

In the program I had (already) included the following:

if r < (sd) then {avoid calculate the field of a particle in (x,y,z), because r=0 end field too big }
begin
r:=sd;

Before: sd=1E-10; {smallest distance between particles to calculate B & E, Bohr radius is 0,53E-10 m}

Now we make: sd=1E-3;

In this way I try to avoid that the particles obtain too high speeds. Muliplying their charge and mass with 1E10 will not make a accurate simulation. But what I like to try out is if the electron cloud and the D+ ion cloud interact between each other.

Experiment 11.15f

Fig.8.

During the time lapse of 8,85E-7 s about 50 D+ ions escaped and some electrons.

Experiment 11.15g

Fig.9.

200 * 1E10 electrons are generated and 150*1E10 D+ ions.

if r < (sd) then {avoid calculate the field of a particle in (x,y,z), because r=0 end field too big }
begin
r:=sd;

Before: sd=1E-10; {smallest distance between particles to calculate B & E, Bohr radius is 0,53E-10 m}

Now: sd=1E-2;

If the distance between particles > 2 cm, then the normal electromagnetic forces are calculated. If the distance is smaller, then, to avoid too big forces, the distance r = 2 cm.

In the time lapse of 3,68E-6 s 1 D+ ion escaped. A lot of electrons escaped.

Fig.10.

One night running. A few D+ escaped and some more e- escaped.

Results so far:

If we simulate only a couple of hundreds of electrons and deuterium ions, they stay nicely confined, at least during the (short) simulation time lapse.

If we increase the mass and charge of each particle, converting it into a kind of group of particles (1E10 particles), then the confinement is less.
This is understandable because electrons repel each other, and the same happens with deuterium ions.

But if we concentrate 1E10 particles in one point, and the came near to each other, very big forces are calculated and they can gain huge speeds.
This is probably the reason why many particles escaped.

In experiment 11.15g we only made normal calculations if the distance between particles > 2 cm. Now we saw less particles escaping.

Still not very clear is yet if the simultaneously presence of negative electrons and positive deuterium ions improves the confinement.

More or less the behavior of the "increased particles" (1E10 concentrated in one) is more or less the same as before, when we simulated normal electrons and deuterium ions.

Further simulation experiments will perhaps be carried out.

Experiment 11.15g

Fig.11.

With normal electrons and D+ ions.
With d(top and bottom sphere)=73 cm and v_D+=4E6 m/s the D+ also stay confined. (middle ring = 140 V).

The same configuration but each "particle" = 1E10 electrons or D+ ions, and if r>1E-2 m then r=1E-2 m (to avoid too big forces when these "particles" are very near each other): The D+ still stay confined but more or less 70 % of the electrons escaped.

Fig.12.

A little bit similar configuration, with the distance of the blue rings a little bit greater to avoid the electrons to escape.
Each "particle" = 1E10 electrons or 1E10 D+ ions, and if r<1E-2 m then r=1E-2 m (to avoid too big forces when these "particles" are very near each other): The D+ stay more or less confined as do the electrons. Only 2 D+ escaped and a few electrons, during the (small) time lapse of the simulation.
In the beginning the max. radius of the D+ and the electrons slightly increased, as did the total energy of all particles. After t=2,6E-6 s the integration time dt was decreased to dt=1E-11 s (was dt=1E-10 s) and these values stayed more or less constant.