11.16 Trying to calculate the possibility of fusion


     A new idea to obtain clean fusion energy         

Home  Introduction  Calculations  Videos  Facebook  Contact   Sitemap

11.16  Confinement of positive ions and electrons with a static electromagnetic field

Sitemap    Trying to calculate the possibility of fusion

---

Let's take for the dimensions of the SEM fusor's vacuum chamber  1 mtr x 45 cm diameter = 1 . π.(0,45/2)2 = 0,16 m3

Suppose we made a good vacuum (1.10-6 Torr) and filled the vacuum chamber again with deuterium gas up to a pressure of 30 microns (3.10-2 Torr).

1 Torr = 1000 microns,  1 micron = 1e-3 Torr = 1E-3 Torr   =  10-3 Torr
1 atmosphere=1013 mbar=760 Torr (mm of Hg) = 760 000 micron (millitorr, mTorr ) = 101325 pascal (N/m2)        1 bar = 100 000  pascal      e-2 = E-2 =10-2   

 1 J = 2,6e-8 ltr diesel   ( hypertextbook.com )

(see: http://www.fusor.net/board/viewtopic.php?f=42&t=10776 )

How many D atoms we have now ? (with a pressure of 3.10-2 Torr)

Ideal gas law:  p.V = nRT

p = pressure of the gas (Pa or N/m2 )      (1 torr = 1/760 atm = 133,3 Pa)  -> 3E-2 torr =    4,0 N/m2
V = volume of the gas ( m3)
n = amount of substance of gas (in moles)
R = ideal gas constant = 8.3144598 J.mol-1.K-1 

Let's take for the temperature T = 293 ºK

-> n = p.V / R.T = 4,0 .0,16 / (8,3145 . 293  ) = 2,63E-4 mol   (1 mol = 6,022 E23 molecules D2)

2,63E-4 . 6,022 E23 = 1,58 E20 molecules D2  (3,16E20 ions D+)  => density = 1,58 E20 molecules/0,16 m3 = 9,88E20 molecules/m3 = 1,98E21 D ions /m3

In Wendelstein7-X a plasma density of of 3.1020 particles per cubic metre is aimed.

massa deuterium ion D+ = 2 . 1,67E-27 kg = 3,34E-27 kg

Total massa deuterium in the vaccum chamber = 1,58 E20 . 2. 3,34 E-27 kg = 1,06E-6 kg  (1 mg  molecules D2 )

 100 kWh = 9,4 ltr diesel = fusion energy of 4,1 E-3 gram of deuterium (see Droom11.html# )

1,06E-6 kg deuterium is equivalent with  (1,06E-6) / (4,1 E-6) . 9,4 = 2,43 ltr diesel.

This is some amount of energy, not so much, but at least our vacuum chamber will not be a potential "nuclear bomb" , which is an advantage.

---

The nuclear force is powerfully attractive between nucleons at distances of about 1 femtometre (fm, or 1.0 × 10−15 metres), but it rapidly decreases to insignificance at distances beyond about 2,5 fm.

How much energy does it cost to bring two deuterium ions at a distance of 1 femtometre?

  Z  = 1  (amount of positive protons in a deuterium ion)
  k is the Coulomb's constant = 9,0×109 N m² C−2
  1 eV = 1,6 . 10 -19  J    
   = >  Ucoul =  k . Z  . Z  . e 2  / r  =  9.0 . 10 9 . 1 . 1 . (1,6.10 -19 ) 2  / (1.10 -15)  =  2,3 .10 -13   Nm  = 1,44 MeV             

    (see: wiki/Coulomb_barrier )

The kinetic energy of one D+ ion (with massa m and speed v) = 0,5.m.v2 = 0,5. (2 . 1,67 . 10-27) . v2  =  2,3 .10 -13   J 
   =>   v =  11,8 . 10 6  m/s   (T = 1,1.1010 K )

So to overcome the Coulomb barrier and one D+ ion has no speed, the other one must have a speed of   11,8 . 10 6  m/s  (collision head on, according this simplified calculation).

If the two D+ ions have opposite speeds: 0,5.m.v2 + 0,5.m.v2  = (2 . 1,67 . 10-27) . v2  = 2,3 .10 -13   J  =>  they must colide with 8,3 .106 m/s .

(1/2).m.v2 = (3/2) . kB .T   kB = 1,38.10-23 J.K-1)      -> T = 1/3 . m(D+ ion) .  (8,3 .106)2  . / kB =  5,6.109  K

http://www.splung.com/content/sid/5/page/fusion

--

In alpha.web.cern.ch/penningtrap a device  a little bit simular to the SEM fusor is used, but not for fusion. Here the goal is to trap antiprotons and positrons in order to produce antihydrogen. According to them the electrons cool down due to cyclotron_radiation .  "Antiprotons, however, are far more massive. It would take antiprotons over 300 years of sitting in a 1 Tesla magnetic field to cool through cyclotron radiation alone!" That the electrons cool down in the SEM fusor is only favorable, I think. So they form even better a negative cloud: a virtual cathode (I suppose). The protons (D+ ions) however should be hot, move with high speeds in order to be able to fuse.

--

When any charged particle (such as an electron, a proton, or an ion) accelerates, it radiates away energy in the form of electromagnetic waves. For velocities that are small relative to the speed of light, the total power radiated is given by the Larmor formula:
(see: /hyperphysics.phy-astr.gsu.edu/hbase/particles/synchrotron.html and Larmor Formula )

P = 2Kq2a2 / (3c3)

K = Coulomb's constant = 8.987.109  Nm2/C2
 a = the  accelaration of the particle
q = the charge of the particle
c = the speed of light = 3.108 m/s

The charge for both the electrons and the deuterium ions is 1,60E-19 C

Let´s take for the mean speed 2E6 m/s   (more or less the speed necessary for fusion,  see  Droom11.html#  )

B = 1 tesla (strength of the magnetic field)

B.v.q = m.v2 / r  = m .a   (see: Droom11.html#Fig._4 )
v = speed
a = acceleration (centripetal)
m = mass of the particle

Energy loss of an electron due to the magnetic field

a electron = B.v.q / m = 1. 2E6 . 1,6E-19 /(9,1E-31) = 3,52E17 m/s2

=> P electron =  2 . 9E9 . (1,6E-19 )2 . (3,52E17)2 / (3(3E8)3)  =    57,095E6 / 8,1E25 = 7,049E-19    J/s

kinetic energy of an electron = 0,5.m.v2  = 0,5 . 9,1E-31 . (2E6)2 = 1,82E-18 J

Due to the centripetal acceleration caused by a magnetic field of 1 tesla, an electron with a speed of 2E6 m/s would lose in about 2,6 s its kinetic energy.

 

Energy loss of a deuterium ion due to the magnetic field

aD+ = 1 . 2E6 . 1,6E-19  / (2.1,67E-27 ) = 9,58E13 m/s2

=> PD+ =  2 . 9E9 . (1,6E-19 )2 . (9,58E13)2 / (3(3E8)3)  = 4,229 / 8,1E25 =  5,22E-26 J/s  

kinetic energy of a D+ ion  = 0,5.m.v2  = 0,5 .(2 . 1,67E-27 )  . (2E6)2 = 6,68E-15 J

Due to the centripetal acceleration caused by a magnetic field of 1 tesla, a deuterium ion with a speed of 2E6 m/s would lose in 1,3 E11 s  (4058 year!) its kinetic energy. Negligible

Energy loss of a deuterium ion due to the electrostatic field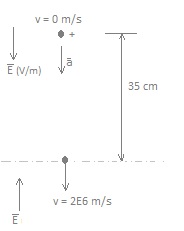

Let's consider the configuration of  #Fig.7a .

The deuterium ions move vertically up and down covering a distance of about 70 cm.

Suppose a D+ ion has in the centre a speed of 2E6 m/s and when reached a vertical distance of 35 cm from the centre, its speed is zero.

Formulas of motion:
0,35  = 2E6 . t +  0,5.a.t2
0  = 2E6 + a .t

a = -2E6 / t
0,35 = 2E6 . t + 0,5.-2E6 . t  => t = 0,35 / (1E6 ) = 3,5E-7 s  and  |a| = 5,7E12 m/s2

This is a mean (de)acceleration. In reality it will not be constant, but for simplicity let's assume the (de)acceleration is constant, only switching from direction (sign) when passing the centre.

The mean acceleration due to the electric field is smaller than the one due to the magnetic field, and therefore the energy loss due to this acceleration is also negligible..

Conclusion

=> The energy loss (Larmor formula) of the deuterion ions due to the accelerations caused by the magnetic and electric field of the SEM fusor is neglibible ☺

=> The electrons loose quickly their kinetic energy according the Larmor formula.

---

Lawson's criterion

Confinement time is the time the plasma is maintained at a temperature above the critical ignition temperature.

For deuterium-deuterium fusion: n. τ ≥ 1016  (s/cm3)  ( see the link above)

n = ion density in the plasma

We already calculated before that in the vacuum chamber of our SEM-fusor
(1mtr x 45 cm diameter ) with a pressure of 3E-2 torr there would be 1,58 E20 molecules D2. Suppose they are all ionized, then we would have 3,16E20 D+ ions.

Suppose this is our ion density in the plasma and the temperature is above the critical ignition temperarure

=>  n = 3,16E20 / 0,16 = 1,975E21 ions/m3 = 1,975E15 ions/cm3

=> τ ≥ 1016 / (1,975E15)  = 5,1 s

---

https://en.wikipedia.org/wiki/Migma#Problems

Two possible energy losses:

Electrons and D+ ions collide and neutralize, meaning they are no longer subject to the elecric and magnetic field and leave the reaction chamber.

Collisions between D+ ions and electrons will give energy to the electrons which will be released by bremsstrahlung/synchroton radiation.

---

In https://en.wikipedia.org/wiki/Solar_core

"At the center of the Sun, fusion power is estimated by models to be about 276.5 watts/m3. Despite its intense temperature, the peak power generating density of the core overall is similar to an active compost heap, and is lower than the power density produced by the metabolism of an adult human."

And here: coldfusionnow.org/power-equivalent-to-the-sun-we-already-have-it/

---

How much energy is stored in an operational SEM fusor?

Suppose the mean speed of the  D+ ions is v = 2E6 m/s (speed needed for fusion, see Droom11.html# )
The vacuum chamber of 1mtr x 45 cm diameter with a pressure of 3E-2 torr contains 3,16E20 D+ ions (already calculated before).
m(D+ ion) = 2 . 1,67E-27 kg
Total kinetic energy = amount of  D+ ions  .  ½ m(D+ ion) v2   =  3,16E20 .  ½ .( 2 . 1,67E-27). (2E6 )2   = 21,1E5 J  (1 J = 2,61E-8 ltr diesel. see energy_conversion_calculator   => 55. 10-3 ltr diesel , 47 gram)
The kinetic energy of the electrons is neglible because of their small mass.

The energy per unit volume in a region of space of permeability, μ0, containing magnetic field, B, is:  u =  ½ . B2 / μ0,    ( see wikipedia.org/wiki/Magnetic_energy )

B = 1 tesla =>  u = 0,5 . 1 / (4 π 10-7 ) =  4,0.105  J/m3

Vaccuum chamber SEM fusor = 0,16 m3 =>  magnetic energy = 6,4 .104 J   (1,7.10-3  ltr diesel , 1,5 gram)

The electric energy stored in one of the charged spheres (see  Droom11.html#Fig._7a ) :
E  = ½ QV
V = 250 kV = 9E9.Q /r
r = 6 cm
=> Q = 1,67E-6 coulomb

=> E  =  ½ . 1,67E-6 . 250E3 = 0,21 J ( 5,4E-9 ltr diesel)  

A system of point charges also has a potential electric energy, see  experiment9.html.

Let's calculate how much energy it costs to bring one of the spheres of the Sem fusor from infinity to a distance of 1 m from the other one (distance between their centres).

E = Q . 9E9 . Q / 1 = (1,67E-6) .9E9 . (1,67E-6) = 0,025 J , which is neglectable.

The potential energy of the rings and spheres together will also be neglectable (the energy it would take to bring them from infinity together into the Sem fusor configuration).

We have totally 2 charged spheres and 3 charged rings, so the estimated total electrical energy will be approximately  5 x 0,21 J = 1,05 J  (2,6E- 8 diesel). 

=>  Most of the energy is stored in the kinetic movement of the D+ ions.  The electrical energy of the charged spheres and rings and the magnetic field is relatively small.

 

Facebook
sem-fusor.com

 

Sitemap28 January 2018      by  Rinze Joustra        www.valgetal.com