|
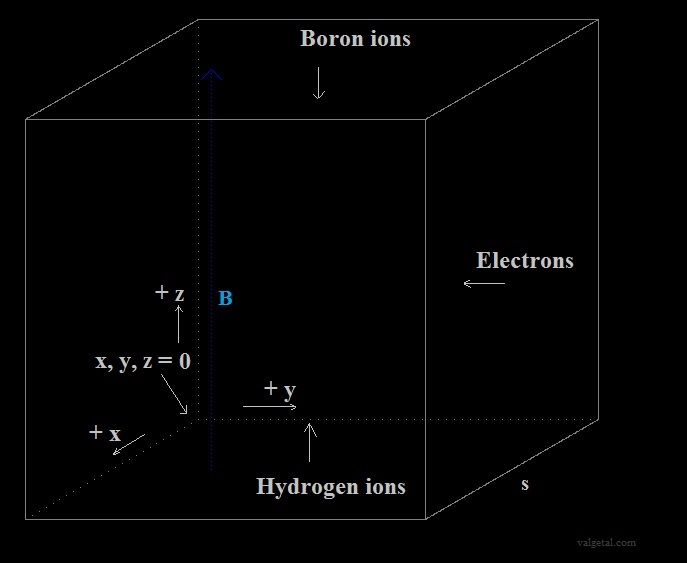
Fig. 1 The coordinate system
The program is programmed in Delphi 4.
We use above displayed coordinate system.
The sides of the cube are s (s=400 pixels = 1 mtr).
The electrons can be injected in any point (we will do this in such a way
that they circle around the centre of the cube).
Actually we could inject any particle with any velocity
in any point...
A magnetic field is introduced in the program. A positive value means that the
magnetic field B is pointed up and is homogeneous.
(we can B also make variable, for example less in the centre and higher at
the sides and near the top and the bottom)
In the program we calculate the electric field and the
magnetic field in point (x,y,z) due to a charged moving particle in point
(xi,yi,zi) (for non relativistic v<<c) and adding the fixed
magnetic field and electric field.
The electric field in a point (x, y, z): ( See
Coulomb's law )

The magnetic field we calculate with
Biot-Savart Law.
(for v<<c)

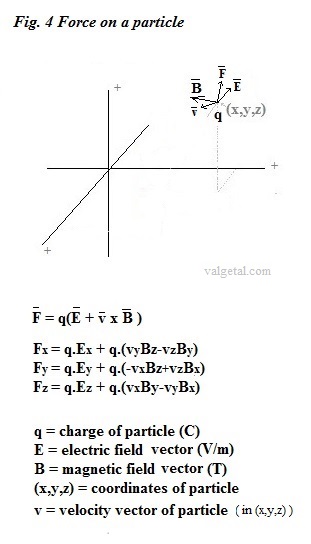
Lorentz force
How many electrons
produces an electron gun?
A Nanocoulombmeter in
combination with a Faraday cup can
be used to detect and measure the beams emitted from
electron
guns and ion guns.
(
http://en.wikipedia.org/wiki/Nanocoulombmeter
In the link below an electron gun
is sold with an energy range: 1 eV to 100 keV and a beam current range: 1 nA
to 20 mA
(
http://www.kimballphysics.com/electron-gun-systems/product-overview )
1.10-9 A
= 1.10-9 C/s -> 1.10-9 C/s
/ (1,6.10-19 C) = 6,3. 109 electrons/s
It seems
therefore plausible to have an electron gun that produces about 6.3. 109
electrons/ s
This is 1 electron/1,59 10-10 s
If the energy of an electron is 1 eV, than:
― meVe2
= 1 eV = 1,602.10-19
J =>
Ve =
√ (2 . 1,602.10-19
/ (9,1095
. 10-31) ) = 5,931.
105
m/s
---------------
Suppose you have a boron ion with an energy of 4 MeV.
What magnetic field is needed to deflect this ion into a circle with a
radius of 0,5 mtr?
B= m .v / (r . q )
― mv2 =
4
.106 .
1,6.10-19
J
=> v =
√ (2 . 4
.106
1,6.10-19
/ (11 .
1,67
. 10-27) )
=
8,35.106
m/s (boron = 5 proton + 6 neutron,
relativistic effects neglected)
=> B =
(11 . 1,67
. 10-27) .
8,35.106
/ (0.5 .
1,6.10-19
) = 1.9 tesla, if it's charge
is e+ and B = 0,38
tesla if it's charge is 5e+
According
en.wikipedia.org/wiki/Orders_of_magnitude_(magnetic_field)
this (2 T) is a magnetic field generated in
a
modern 60
Hz power
transformer.
The remanent field of a neodymium magnet is typically about 1-1.4 tesla,
see
en.wikipedia.org/wiki/Neodymium_magnets
To construct a electromagnet of 2 Tesla seems to be a bit
difficult, see instructables.com/answers/2-Tesla-Electromagnet/
Already simulations of plasma behaviour has been made,
see:
https://en.wikipedia.org/wiki/Particle-in-cell
---------------
Video of computer simulation
Experiments with the program:
| If r < (1E-8) then avoid calculate the field of a particle in (x,y,z),
because r=0 end field too big
Experiment 1:
10 Boron+ ions started with speed=0 above at (x=0,5s,
y=0,5s, z=0,75s) and 10 H+ ions started with speed=0 below at (x=0,5s,
y=0,5s, z=0,25s), see fig. 1 for coordinate system. Click in the image for a
full screenshot.

First the electrons moved together in a circle. Later on
they separate in three different circles.
Also curious is that a few H+ and B+ ions obtain more kinetic energy because
they move more up and down (farther away) than there initial positions. It
seemed to be that they collided amongst themselves. Curious, because the
possibility of colision was not programmed.''
The same experiment, but more time elapsed:
 |
Experiment 2:
3 Boron+ ions started with speed=0 above at (x=0,5s,
y=0,5s, z=0,75s) and 3 H+ ions started with speed=0 below at (x=0,5s,
y=0,5s, z=0,25s).
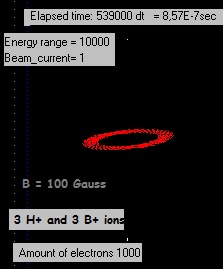
The electrons were obtaining more speed (kinetic energy); in some
configurations (B-field, initial speed etc.) they quite rapidly
increased their radius. So a new procedure was introduced in the
program: if (the total kinetic energy of all electrons ) - (initial
kinetic energy of all electrons) > 10-14 J , then the speed of all
electrons is decreased untill the difference <10-14 J |
Experiment 3:
3 Boron+ ions started with speed=0 above at (x=0,5s,
y=0,5s, z=0,75s) and 3 H+ ions started with speed=0 below at (x=0,5s,
y=0,5s, z=0,25s).
 The electrons start to spread upwards and downwards. Itīs a pity,
but they do not keep nicely moving in a circle.
The electrons start to spread upwards and downwards. Itīs a pity,
but they do not keep nicely moving in a circle.
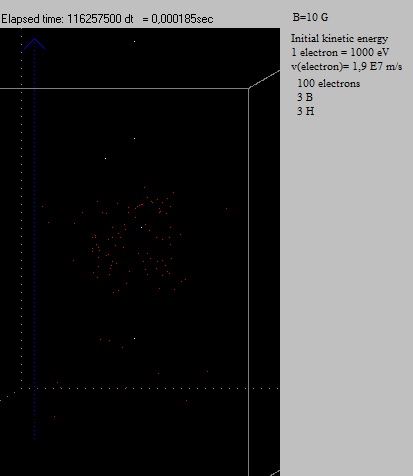 The
same experiment, but a few days later. The electrons did spread even
more, although still moving in circles around the z-axis. The
same experiment, but a few days later. The electrons did spread even
more, although still moving in circles around the z-axis. |
| |
Experiment 4:
3 Boron+ ions started with speed=0 above at (x=0,5s,
y=0,5s, z=0,75s) and 3 H+ ions started with speed=0 below at (x=0,5s,
y=0,5s, z=0,25s).
 One
B+ and 1 H+ have disappeared (out of screen), One
B+ and 1 H+ have disappeared (out of screen),
probably because collision and obtaining a high speed.
Also curious there has appeared a gap in the ring with electrons. |
Experiment 5:
Instead of electrons, 20 Boron+ ions,
circulating with the clock. The B field is first 10000 G, and then
increased to 16000 G.
%20%20about%2018%20hrs%20working%20klein.jpg) |
Experiment 6:
30 electrons, 100 eV, 0,001 nA, 3 B+, 3 H+, B=10 G, after about 15
min (just generated all 30 electrons), increased the field to B=100
G, resulting in a kind of "pulsating circle" of electrons, which
seems to be not spreading out...

More about experiment 6
(and 7) |
Experiment 7:
50 electrons, 100 eV, 0,001 nA, 3 B+, 3 H+, B=10 G, after about 30 min (just generated all
50 electrons), increased the field to B=100
G
In reality it will not be possible to change the magnetic field
instantaneously, because, if we use an electromagnet,
it will have an selfinductance which will delay the building up of a new
magnetic field..
Therefore we simulate this by distributing the electrons randomly
inside a circle determined by the old and the new B-field
(see
More about experiment 6 &7
)
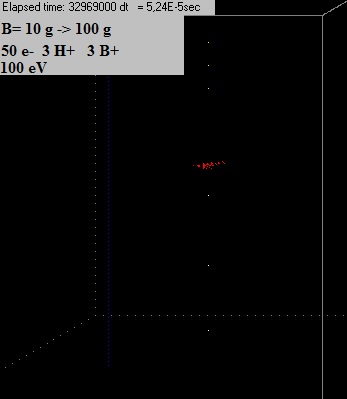
Video experiment 7
(after 5,18E-5 s)
After 5,18E-5 sec, about 8 hrs computer time, the
electrons still did not spread out..
Video experiment 7
(after 0.000173 s)
And after 0,000173 s neither.... (remark: in the program the
total kinetic energy of all electrons is checked all the time, and
stays constant; when it increases to much, the speed of each
electron is multiplied with a factor 0,999 untill itīs again within
limits)
Video experiment 7
(after 0.00021 s)
Video experiment 7
(after 0.00036 s) A few electrons are now a bit farther away from
the centre.
Video experiment 7
(after 0.00037 s) They came again a little bit closer to the
centre.
Video experiment 7
(after 0.000596 s) 1 or 2 electrons have escaped out of the
chamber. The rest are still ubicated in the centre, but seemed to
have slowed down and moving in small circles. In the program the
total kinetic energy of the electrons cannot increase. If it
increases a little bit then the speed of each electron is
multiplied with 0.999 in a repeat loop, until the present total
kinetic energy of the electrons < initial total kinetic energy. But
the total kinetic energy can yes decrease, and that is probable what
has happened (due to the fact the this simulation is an
approximation of reality, the same way you can approximate a smooth
line by a stepwise drawn line... |
| Experiment 8:
In the former experiments we generated the electrons in a point of
their orbiting circle inside the vacuum chamber. In reality not very handy to let the electron
gun point inwards the vacuum chamber were fusion should take place.
Letīs now see if it is possible to generated them in point (0,5s, s,
0,5s), in the middle of the right side, and let them again orbit in
a circle around the centre of the cube...
More about experiment 8 |
| Experiment 9: From experiment 3
the total kinetic energy of all particles can not increase (when it
increases beyond a limit, the speed of the electrons is reduced a
bit until itīs again under this limit). The kinetic energy can
however yes decrease, and this is what possible happened in
experiment 7. Now in experiment 9 it can neither decrease.
Furthermore the potential energy is calculated .
More about experiment 9 |
| Experiment 10: The simulation
program has been refined by implementing the Leapfrog intergration
method.
More about experiment 10 |
|
Only positive ions (H+, B+) are released in the vacuum chamber
(no electrons): above and
under positive point charges are placed and a vertical magnetic
field is applied. The goal is to confine the positive ions.
Experiment
11 |
20 February
2014 -.
by
Rinze
Joustra www.valgetal.com

|




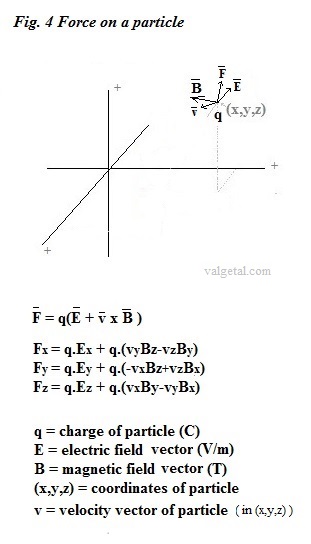






%20%20about%2018%20hrs%20working%20klein.jpg)

