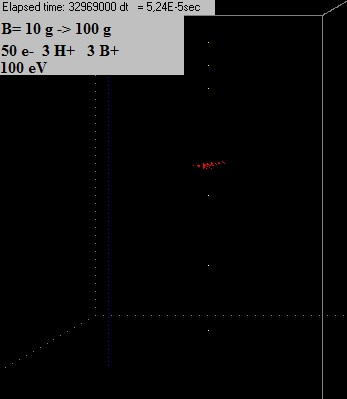
10.6 & 10.7 Physics experiment: simulation of moving electrons, hydrogen and boron ions in a magnetic field
 Computer simulation of idea 10
Computer simulation of idea 10
Experiment 6 & experiment 7
| Experiment 6:
B=10 gauss
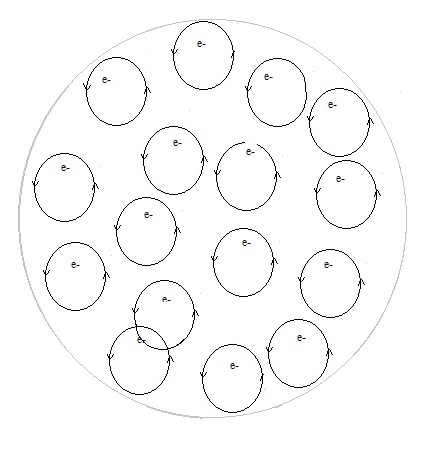
Experiment 6 video (after 0,000141 sec) Experiment 6 video (after 0,00037 sec, some computer time hours later) Experiment 6 video (after 0,00056 sec, about 24 computer time hours later) (looks like not any difference, electrons do not spread out)
|
An intuitive way of explaining this:
First the electrons move in a (big) circle. When we increase the magnetic field, they start to move in smaller circles, see figure 1.
Fig. 1
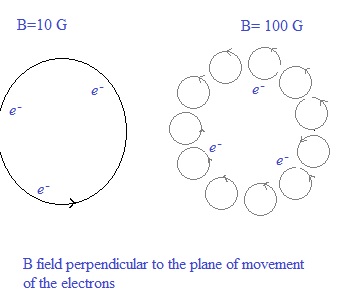
Each electron moving in a small circle could be considered a small magnet.
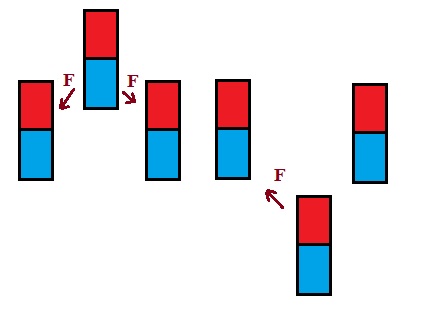
What happens if an electron moves up or down, in vertical direction?
Perhaps the south poles get attracted by the north poles which prevent that they
leave the plane in which they are moving, see figure 2.
Fig. 2
But what about leaving in a horizontal direction?
Fig. 3
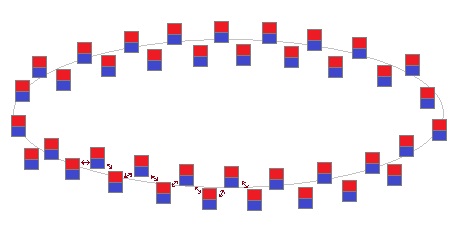
If all the small magnets (electrons moving in a small circle) are alternately
a little bit upwards and downwards positioned, then the forces
between them will
prevent them both to move away up or down, and to move away in a horizontal
direction.
Just trying to explain... Anyway, in the simulation, as already mentioned, they seem not to spread out....
Experiment 7:
In reality it will not be possible to change the magnetic field
instantaneously, because, if we use an electromagnet,
it will have an selfinductance which will delay the building up of a new
magnetic field..
After having increased (slowly) the magnetic field, the situation would be as
ilustrated in figure 4 (if I am not wrong...)
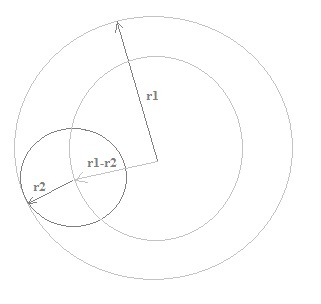
Imagine an electron moving in the big circle. Then the B-field increases a
little bit, so the electrons move a little out
of the big circle towards the centre, moving in a circle with a slightly smaller
radius. Then the B-field increases again a little bit,
and the electrons will move in a new circle with again a slightly smaller radius
etc.
Fig. 5
First the electrons move in the big circle due to magnetic field B1 -> r1= m.v /( q.B1) (m= massa electron, v = speed electron, q = charge electron)
Then we increase the field to B2 -> r2= m.v /( q.B2)
We will adapt the computer program: when the B field changes, we will
distribute the electrons randomly inside the circle with radius r1-r2 .
Fig. 6
Fig. 7
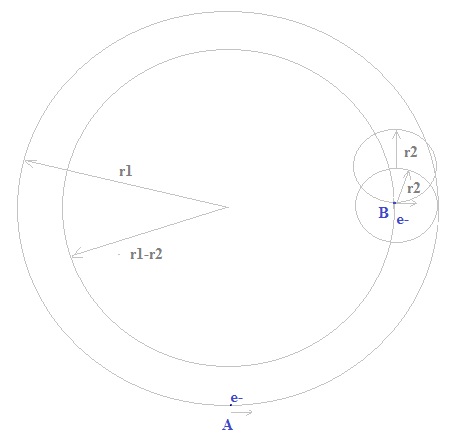
In the program we choose r and f randomly. r = r1 - r2. See fig. 5 & 6. The field B can only be increased (otherwise an error in the program).
Each electron is thus distributed randomly inside the circle with radius r.
Not correct: the program could take the electron in point A and put it in point B, but the velocity stays the same. Then this electron could go (a little bit) outside the circle with radius r1, and in reality this can not happen. Every time the B increases, the electron will move in a circle with a smaller radius. Thus in a circle inside the former circle... and can never go outside the first circle.
Not correct: when the program randomly distributed the electrons, its electrical potential (Coulomb's law) could increase, but the total kinetic energy of the electrons stays constant.
Correct should be to change the magnetic field during, for example1 second, and let the program run. But the program runs so slowly, that we should have to wait 80 years... (1000dt is about 1 second computer time if there are 50 electrons).
Anyway the program in experiment 7 seems to demonstrate that a collection of 50 electrons moving in small circles stay "together" in a " simple " magnetic field.
Remark: the magnetic field in the centre of the cube is 1E2 gauss, and at the sides, top and bottom a little but larger (1,1E2 gauss).
|
1.10-9 A during 10 s = 1.10-9 Q/s .10 s / ( 1,16.10-19 Q/s) = 8,6.1010 electrons. A lot more than in the program, and impossible to simulate with it...
|
||
|
|