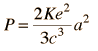10 Breaking the Coulomb barrier by electrostatic acceleration of positive ions towards electrons moving in a circle
(10e idea)
|
The goal is to design a kind of
fusor
(
http://en.wikipedia.org/wiki/Fusor ). But instead of a fixed inner grid, which causes
losses, we try to create a kind of negative potential well by injecting
electrons inside the sphere. In the
polywell
also electrons are injected. Here several magnets try to keep the
electrons confined inside the sphere. Let us
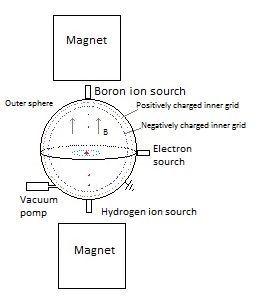
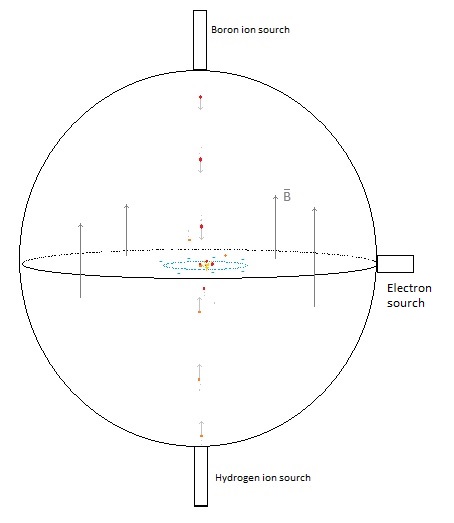
now consider the following device with only two magnets: Fig. 1. Schematic
representation of an electrostatic magnetic fusion device.
The (outer)
sphere has been pumped vacuum and is earthed. Above
and under the sphere a magnet is placed which generates an (approximately)
uniform (vertical) magnetic field inside the sphere. With an
electron source (electron gun) we shoot electrons in a horizontal plane
inside the sphere. Because
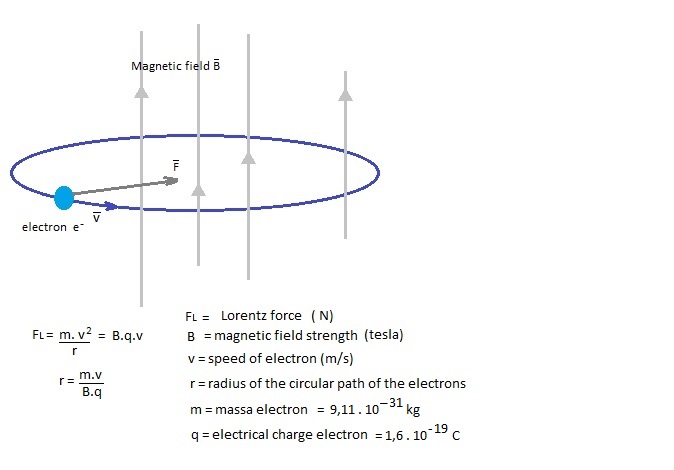
of the magnetic field the electrons will move in circles. Fig. 2. Circular
movement of electrons in an uniform magnetic field
In an electron gun the
electrons are accelerated till about 30 keV ½ m.v2
= 30.103.1,6.10-19
J => v =
√ (2.30.103.1,6.10-19
/ (9,11.10-31 )) = 1,0.108 m/s
( speed of light
is 3,0.108 m/s) If we
want the electrons to circulate in an orbit with a radius of, for example, r
= 2 cm, then we need a magnetic field of: B = m.v / (r.q) = 9,11.10-31.1,0.108 / (0.02.1,6.10-19 ) = 2,8. 10-2 T = 280 gauss (actually we should also have taken into account relativistic effects...) This is
still less than a loudspeaker magnet, so we do not need strong magnets.
(http://en.wikipedia.org/wiki/Orders_of_magnitude_(magnetic_field) ) But I don't think it's necessary that the electrons have such a high speed. Let's take 100 eV. v =
√ (2.100.1,6.10-19
/ (9,11.10-31 ) ) = 5.93.
106 m/s (this is way lower than
the speed of light, so no relativistic effects) Several values:
The classical formula for the radiated power from an accelerated electron is
(1) (see: /hyperphysics.phy-astr.gsu.edu/hbase/particles/synchrotron.html and Larmor Formula )
Let's calculate this for electrons with 100 eV: K= 8.987.109 Nm2/C2 ; c = 3.108 m/s ; e = 1,6.10-19 C
a = v2/r = (5.93. 106)2 / 0.02 = 1.76.1015 m/s2
-> P = 2 . 8.987.109 . (1,6.10-19 )2. / (3.(3.108)3) . (1.76.1015 )2 = 1.76 .10-23 J/s (for 1 electron)
This will cause a decrease in kinetic
energy of an electron in 1 s: Δ ½mv2
= 1.76 .10-23 J
How many electrons produces an electron gun?
A Nanocoulombmeter in
combination with a Faraday cup can
be used to detect and measure the beams emitted from
electron
guns and ion guns.
(
http://en.wikipedia.org/wiki/Nanocoulombmeter
In the link under an electron gun
is sold with an energy range: 1 eV to 100 keV and a beam current range: 1 nA
to 20 mA
1.10-9 A
= 1.10-9 C/s
~ 1.10-9 C/s
/ (1,6.10-19 C) = 6,3. 109 electrons/s
It seems
therefore plausible to have an electron gun that produces about 1. 109
electrons/ sec. The
sphere we give a radius of 25 cm. After 1
s there are 109 electrons inside the sphere and for the
voltage calculation we assume that they are located in the centre of the
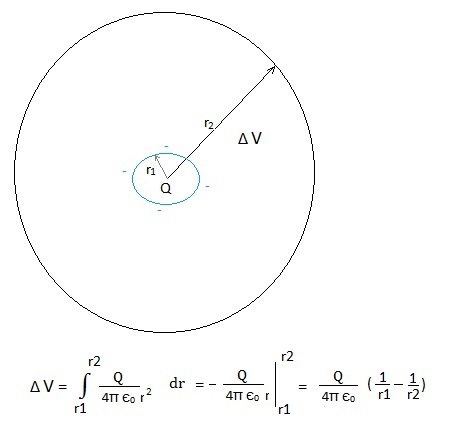
sphere. Fig. 3. Horizontal
cross section with a potential difference ΔV
caused by the accumulation of the electrons
r1 = the radius of the circular
movement of the electrons;
After 1 s we have Q =
109 .
1,6.10-19 =
1,6.10-10 C
(if
no losses; this is like a current of 1,6.10-10 A) r1 = 2,0 cm;
r2 = 25 cm 1/(4π є0)=
9.109 (Nm2/C2)
ΔV = -
1,6. 10-10 . 9 . 109 ( 1/0.02 - 1/0,25)
= - 66,24 V (C.Nm2/(C2
. m) = Nm/C) After
one hour:
ΔV
= 3600 . - 66,24 V =
-2,4 . 105 V And after 4 hours:
ΔV = 4.
-2,4 . 105 = - 9.6 . 105 V ≈
- 1 MV Will the electrons stay
in orbit? How many electrons will escape?
Fig. 4. Positive
charged boron ions and hydrogen ions are shot into the sphere The positive ions move
first parallel to the magnetic field, so they will no feel any Lorentz force
and will keep moving in a straight line. The accumulation of
electrons in the centre causes a negative potential well and the positive
boron and hydrogen ions will be accelerated towards the centre. The moving electrons
generate also a magnetic field that will exert a Lorentz force on the moving
positive ions. We will assume (can this be done?) that the boron and
hydrogen ions still reach the centre area. Some of the ions will
collide and others continue moving straight ahead after which they will be slowed
down because of the negative potential well and move back again towards the
centre area. Some ions will obtain a
higher speed after a collision, and some of these ions collide again and some
of them obtain an even higher speed, and collide again and obtain an even
higher speed etc. And sometimes two
ions, a boron and a hydrogen, with a very high speed collide and fuse in the
boron-hydrogen
fusion reaction:
115B + 11H -> 3 42He + 8,68 MeV (see en.wikipedia.org/wiki/Aneutronic_fusion) No noxious neutrons are produced and the 3 positive 42He+ particles will move with high speed out of the centre increasing the voltage.
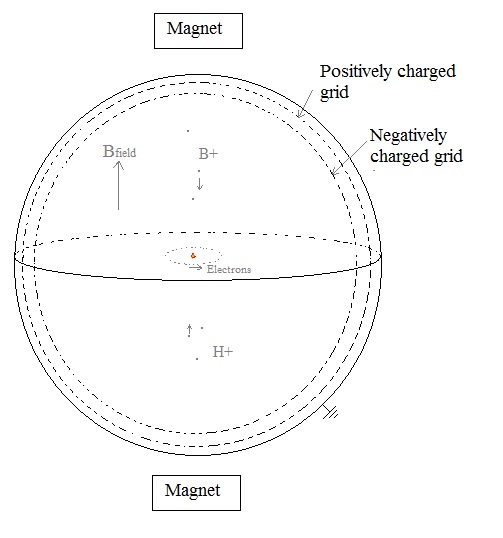
Inside the sphere, we
place two grids. The first grid with a diameter of 22 cm we charge
negatively with a potential
of (for example) -9 MeV, and the second grid with a diameter of 24 cm is
(for example) + 100 V positively
charged
Fig. 5. The sphere with two grids
With these two grids and the applied voltage we try to avoid that any high energy boron or hydrogen particles escape, and we stop the 42He2+ particles transferring their kinetic energy into electric energy (after fusion they will escape with 8.68 MeV).
But the incoming positive ions of boron
and hydrogen should not go through the voltage difference between the two
grids. They would increase speed, which would be positive, but the invested
energy is difficult to recover..
Perhaps we let them travel through a conducting pipe the first part? Some ions could collide with the grid and this would cause energy looses. How much?? Computer program: Keep thinking about this.. ☺
|
|||||||||||||||||||||
|
|